Решение прямоугольного треугольника
Выведенные нами соотношения дают возможность решать прямоугольные треугольники, т.е. по некоторым данным элементам треугольника находить все остальные.
Рассмотрим несколько примеров.
1. Даны гипотенуза прямоугольного треугольника и один из его острых углов. Найти катеты этого треугольника и второй острый угол.
Пусть гипотенуза с = 82,0 см; ∠А = 42°. Вычислить длину катетов а и b и величину угла В.
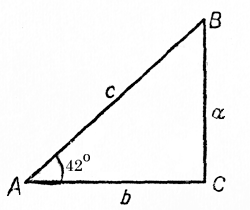
Прежде всего определим величину ∠B,
∠В = 90o - ∠А = 90° - 42° = 48°.
Чтобы вычислить длину катета а, найдём по таблицам значение синуса угла в 42°.
sin 42° = 0,6691.
Так как а = с sin ∠А, получим: а = 82,0 • 0,6691 \( \approx \) 54,9 (см).
Второй катет треугольника можно вычислить различными способами. Используя значение угла А, находим: b =с cos 42°, или b = 82,0 • 0,7431 \( \approx \) 60,9 (см).
Все неизвестные элементы треугольника ABC вычислены.
Длину катета b можно найти из равенства b = с sin ∠В, т. е. b = c sin 48°.
Пользуясь таблицами квадратов чисел, можно также вычислить катет b и на основании теоремы Пифагора:
$$ b \approx \sqrt{{82}^2 -{55}^2} $$
2. Даны катет прямоугольного треугольника и один из его острых углов. Найти гипотенузу, второй катет этого треугольника и второй острый угол.
Пусть катет а равен 25 см, угол А равен 32°.
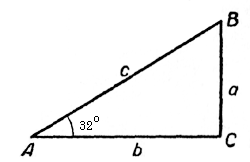
Вычислить длину гипотенузы с, длину катета b и величину угла В.
∠В = 90° - ∠А = 90° - 32° = 58°
а = c sin ∠А, откуда
\( c = \frac{a}{sinA} = \frac{25}{sin32}^o = \frac{25}{0,5299} \approx 47 \)(см);
а = b tg∠А; \( b = \frac{a}{tgA} = \frac{25}{0,6249} \approx 40 \) (см)
Все неизвестные элементы треугольника ABC вычислены. Можно было и в данной задаче применить иные способы решения.
Например: \( b = \sqrt{c^2 - a^2} \approx \sqrt{{47}^2 - {25}^2} \approx \)40 (cм).
3. Даны два катета прямоугольного треугольника, найти его гипотенузу и величину острых углов.
Пусть катет а равен 21 см, а катет b равен 18 см. Вычислить длину гипотенузы с и величину углов А и В.
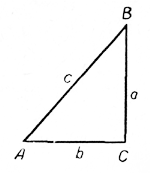
Найдём сначала (пользуясь теоремой Пифагора и таблицами квадратов чисел) длину гипотенузы с:
$$ c = \sqrt{a^2 + b^2} = \sqrt{{21}^2 + {18}^2} \approx 28 (cм)$$
Найдём величину одного из острых углов, используя равенство
$$ \frac{a}{b} = tgA; \Rightarrow tgA = \frac{21}{18} \approx 1,1667 $$Откуда ∠А \(\approx \)49° (с точностью до 1°), тогда ∠B \(\approx \) 41°.