Площадь треугольника

Пусть требуется определить площадь треугольника АВС. Проведём через вершины его С и В прямые, параллельные сторонам АВ и АС.

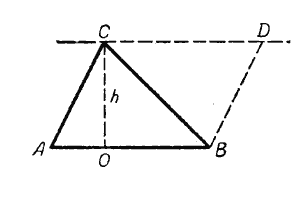
Мы получим параллелограмм АВDС. Площадь его равна произведению основания АВ на высоту СО. Параллелограмм АВDС состоит из двух равных треугольников АВС и ВСD, следовательно, площадь треугольника АВС равна половине площади параллелограмма, т. е. S _{\(\Delta\)ABC} = ¹/₂ АВ • СО.

Отсюда: площадь треугольника равна половине произведения его основания на высоту.

S _\(\Delta\) = \(\frac{a  •  h}{2}\)

Эту формулу можно представить в таком виде:

S _\(\Delta\) = \(\frac{a}{2}\) • h, или S_\(\Delta\) = a • \(\frac{h}{2}\).

Формулы для вычисления площади треугольника

1. Из геометрии известна формула Г е р о н а:

$$ S = \sqrt{р (р - а)(р - b) (р - с)},$$

(где р =^{(а + b + c)}/₂-полупериметр), позволяющая вычислять площадь треугольника по его сторонам.

2. Теорема. Площадь треугольника равна половине произведения двух сторон на синус угла между ними:

S = ¹/₂bc sin A.

Доказательство. Из геометрии известно, что площадь треугольника равна половине произведения стороны треугольника на высоту, опущенную на эту сторону из противоположной вершины.

S = ¹/₂b · h_b (1)

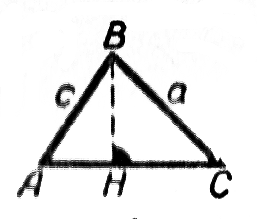
Если угол А острый, то из треугольника АВН найдём ВН = h_b = с sin A.

Если угол A тупой, то

ВН = h_b = с sin (π - A)= с sin A.

Если угол A прямой, то sin A = 1 и
h_b = АВ = с = с sin A.

Следовательно, во всех случаях h_b = с sin A. Подставив в равенство (1), получим доказываемую формулу.

Точно так же получим формулы: S = ¹/₂ab sin C= ¹/₂ac sin B

3. На основании теоремы синусов:

$$ b = \frac{a sinB}{sinA}; \;\; c = \frac{a sinC}{sinA} $$

Подставив эти выражения в формулу (1), получим следующую формулу:

$$ S = \frac{a^2 sinB sinC}{2sinA} $$