Элементы треугольника

1. Треугольник обозначается тремя заглавными буквами, стоящими при его вершинах. Для сокращения записи слов «треугольник» заменяют знаком \(\Delta\). Треугольник, изображённый на чертеже 111, можно записать так: \(\Delta\)АВС.

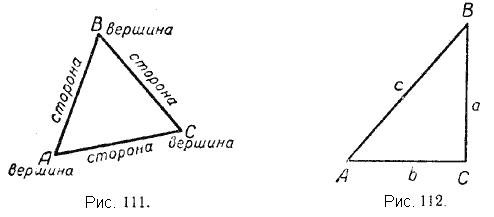
Сторону треугольника принято обозначать той же буквой, что и вершину угла, противолежащего этой стороне, но малой буквой.

Так, например, на чертеже 112 сторона ВС обозначена буквой а, так как она лежит против угла А; сторона СА обозначена буквой b, так как она лежит против угла В; сторона АВ обозначена буквой с, так как она лежит против угла С.

Если продолжим какую-нибудь сторону треугольника, то получим угол, смежный с одним из внутренних углов треугольника. Такой угол называется внешним углом треугольника.

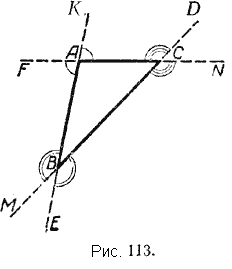
При каждой вершине треугольника может быть построено по два внешних угла (рис. 113).

2. Если из какой-либо вершины треугольника опустим перпендикуляр на противоположную сторону, то получим отрезок, который называется высотой треугольника (рис. 114).

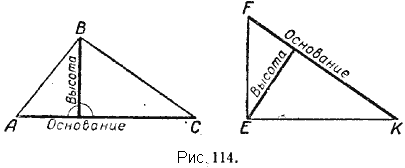
Сторону треугольника, к которой проведена высота, принимают за основание треугольника.

Высота может быть проведена к любой стороне треугольника. Иногда высота треугольника пересекает не само основание треугольника, а его продолжение. Так, на чертежах 115 и 116 высоты AD и ЕМ пересекают продолжения оснований ВС и FK.

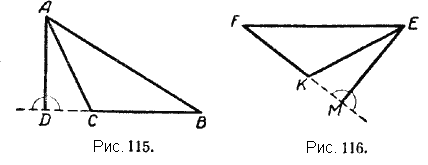
В каждом треугольнике можно провести три высоты. Если аккуратно провести все высоты треугольника, то можно заметить, что все высоты треугольника или их продолжения пересекаются в одной точке (рис. 117, 118).

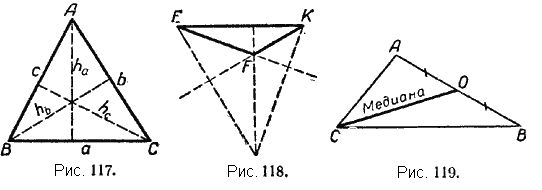
Если же высоты или их продолжения пересекутся не в одной точке, то можно с уверенностью сказать, что чертёж сделан неточно.

Высота треугольника обозначается буквой h, к которой присоединяется обозначение той стороны, к которой она проведена: h_a, h_b, h_c, (рис. 117).

3. Если соединить какую-нибудь вершину треугольника с серединой противолежащей ей стороны, то получим отрезок, который называется медианой треугольника (рис. 119). Медиана обозначается буквой т, к которой присоединяется обозначение той стороны, к середине которой она проведена: m_a, m_b, m_c(рис. 120).

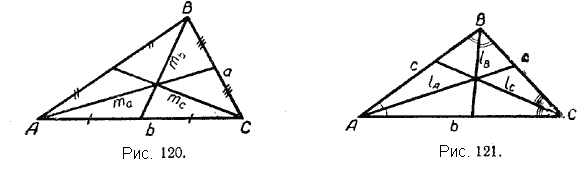
В каждом треугольнике можно провести три медианы. Если проводить их аккуратно, то в любом треугольнике медианы пересекутся в одной точке (рис. 120).

4. Отрезок биссектрисы угла треугольника от его вершины до противолежащей стороны называется биссектрисой треугольника. Биссектриса обозначается буквой l, к которой присоединяется обозначение угла, из вершины которого она проведена: l_A, l_B,l_C (рис. 121), Биссектрисы треугольника (так же как высоты и медианы) пересекаются в одной точке (рис. 121).

Стороны и углы треугольника, а также его высоты, медианы, биссектрисы называются элементами треугольника. Слово «элемент» значит «составная часть».