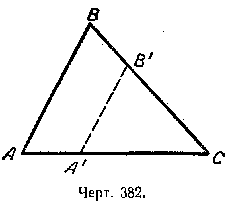Определение подобных треугольников
Рассмотрим два прямоугольных треугольника с острыми углами в 60° и 30° (рис. 364).
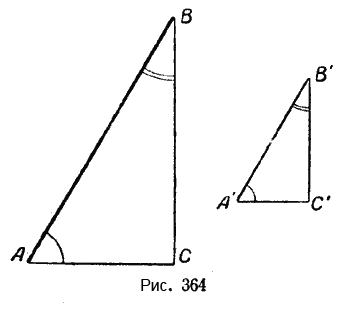
Стороны второго треугольника по сравнению с первым уменьшены в два раза:
\(\frac{AB}{A’B’}\) = 2; \(\frac{AC}{A’C’}\) = 2; \(\frac{BC}{B’C’}\) = 2.
У этих треугольников углы попарно равны. Стороны, лежащие против равных углов, пропорциональны:
\(\frac{AB}{A’B’}\) = \(\frac{AC}{A’C’} = \frac{BC}{B’C’}\) = 2.
Такие треугольники называют подобными. Стороны, лежащие против равных углов, называются сходственными.
Таким образом, подобными называются треугольники, у которых yглы попарно равны, а сходственные стороны пропорциональны.
Подобие треугольников записывается так: \(\Delta\)ABС \(\sim\) \(\Delta\)А’В’С’.
Отношение сходственных сторон подобных фигур называется коэффициентом подобия. В данном случае коэффициентом подобия треугольников АBС и А’В’С’ будет число 2.
Если же взять отношения A’B’/AB = A’C’/AC = B’C’/BC , то коэффициент подобия будет равен 1/2.
Свойство прямой, параллельной какой-либо стороне треугольника.
Проведём в треугольнике АBС прямую DЕ параллельно стороне АС (рис. 365).
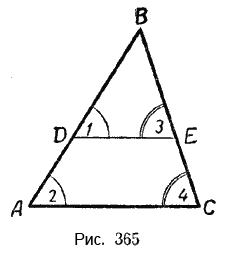
Получим треугольник DВЕ. Докажем, что \(\Delta\)ABС \(\sim\) \(\Delta\)DВЕ.
Вследствие параллельности сторон DЕ и АС ∠1 = ∠2 и ∠3 = ∠4.
Угол В является общим для этих треугольников. Следовательно, углы этих треугольников попарно равны.
Так как DЕ || АС, то \(\frac{AB}{DB} = \frac{BC}{BE}\).
Проведём через точку Е прямую, параллельную стороне AB (рис. 366).
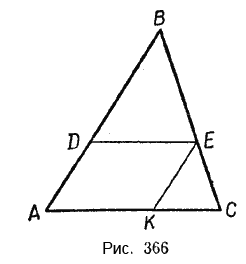
Получим: \(\frac{BC}{BE} = \frac{AC}{AK}\), но АК = DЕ.
Поэтому
\(\frac{BC}{BE} = \frac{AC}{DE}\)
Сопоставляя полученную пропорцию с пропорцией \(\frac{AB}{DB} = \frac{BC}{BE}\) получим:
\(\frac{AB}{DB} = \frac{BC}{BE} = \frac{AC}{DE}\), т.е.
сходственные стороны треугольников AВС и DВЕ пропорциональны.
Раньше было доказано, что углы этих треугольников попарно равны.
Значит, \(\Delta\)ABС \(\sim\) \(\Delta\)DВЕ.
Следовательно, прямая, проведённая параллельно какой-либо стороне треугольника, отсекает от него треугольник, подобный данному.
Отношение площадей двух подобных треугольников
Пусть \(\triangle AВС \sim \triangle A’В’С’\)(черт. 380). Из подобия треугольников следует, что
∠A = ∠A’, ∠B = ∠B’ и ∠С = ∠С’. Кроме того, AB/A’B’ = BC/B’C’ = AC/A’C’.
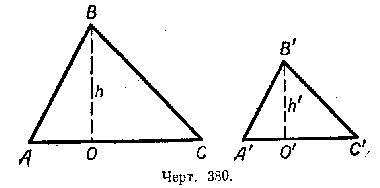
В этих треугольниках из вершин В и В’ проведём высоты и обозначим их через h и h’. Площадь первого треугольника будет равна AC•h/2, а площадь второго треугольника A’C’•h’/2.
Обозначив площадь первого треугольника через S, а площадь второго - через S’ получим: S/S’ = AC•h/A’C’•h’ или S/S’ = AC/A’C’ • h/h’
Из подобия треугольников АВО и А’В’О’ (они подобны, потому что прямоугольные, и, кроме того, имеют по равному острому углу, а именно ∠A = ∠A’) следует:
h/h’ = AB/A’B’ . Но AB/A’B’= AC/A’C’ . Следовательно, h/h’ = AC/A’C’. Заменив в формуле S/S’ = AC/A’C’ • h/h’ отношение h/h’ равным ему отношением AC/A’C’ , получим:
S/S’ = AC/A’C’ • AC/A’C’ , или
$$ \frac{S}{S’} = \frac{(AC)^2}{(A’C’)^2} $$
Итак, площади подобных треугольников относятся как квадраты сходственных сторон.
Полученную формулу можно преобразовать так: S/S’ = (AC/A’C’)2.
Значит, можно сказать, что отношение площадей двух подобных треугольников равно квадрату отношения их сходственных сторон.
Построение подобных треугольников
Мы уже знаем, что для построения треугольника, подобного данному, достаточно из какой-нибудь точки, взятой на стороне треугольника, провести прямую, параллельную стороне треугольника. Получим треугольник, подобный данному (черт. 382):