Свойства равнобедренного треугольника
Построим равнобедренный треугольник ABC и проведём в нём биссектрису угла, заключённого между равными сторонами AB и CB. Равнобедренный треугольник разбился на два треугольника ABD и CBD.
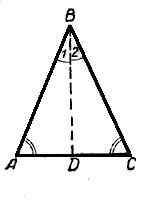
Перегнём мысленно плоскость чертежа по биссектрисе BD так, чтобы правая часть её совпала с левой. Тогда сторона BC пойдёт по стороне BA, так как ∠1 = ∠2, и точка С совпадёт с точкой А, так как BC = BA.
Следовательно, при перегибании чертежа по BD треугольник BDC совместился с треугольником BDA, т. е. биссектриса BD является осью симметрии треугольника ABC.
Отрезки CD и DA совместились, т. е. сторона АС в точке D разделилась пополам.
Следовательно, BD будет не только биссектрисой треугольника ABC, но и его медианой.
Углы BDC и BDA совместились, следовательно, они равны. Но в то же время они смежные, поэтому каждый из них равен прямому углу. Значит, BD является высотой треугольника.
Углы С и А совместились, следовательно, они равны.
Отсюда:
1. Биссектриса угла при вершине равнобедренного треугольника является его осью симметрии.
2. Биссектриса угла при вершине равнобедренного треугольника в то же время является его медианой и высотой.
Так как из вершины треугольника можно провести только одну биссектрису, одну медиану и одну высоту, то медиана, проведённая к основанию равнобедренного треугольника, является и биссектрисой, и высотой, точно так же и высота является и биссектрисой, и медианой.
3. Углы при основании равнобедренного треугольника равны между собой.
4. В равностороннем треугольнике все внутренние углы равны между собой.