Свойство внешнего угла треугольника.
Теорема. Внешний угол всякого треугольника больше каждого внутреннего угла треугольника, не смежного с ним.
Дано: ∠BCD — внешний угол треугольника ABC.
Надо доказать, что ∠BCD > ∠B и ∠BCD > ∠A.
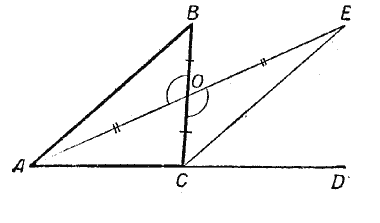
Доказательство. Для доказательства выполним в первую очередь построение, в результате которого внешний угол BCD разобьётся на две части.
1. Проведём медиану АО треугольника ABC.
2. Продолжим её на отрезок OE, равный АО.
3. Проведём отрезок EC.
После этого рассмотрим треугольники AOB и СОЕ. В этих треугольниках
АО = OE и ВО = ОС - по построению.
Углы AOB и СОЕ равны, как вертикальные.
Следовательно, треугольник AOB равен треугольнику СОЕ (по двум сторонам и углу, заключённому между ними, т. е. по 1-му признаку равенства треугольников).
Из равенства треугольников следует, что ∠B = ∠BCE, так как они лежат в равных треугольниках против равных сторон АО и OE. Но угол ВСЕ только часть внешнего угла BCD, поэтому весь внешний угол BCD больше внутреннего угла В. Таким же способом доказывается, что внешний угол BCD больше внутреннего угла А (в этом случае построение надо начать с проведения медианы треугольника ABC к стороне АС).
Из этой теоремы вытекают следствия, важные для доказательства некоторых теорем.
Следствие 1. В тупоугольном треугольнике только один угол тупой, остальные острые, так как внешний угол, смежный с тупым внутренним углом, — острый, поэтому каждый из остальных внутренних углов — тоже острый.
Следствие 2. В прямоугольном треугольнике только один угол прямой, остальные острые, так как внешний угол, смежный с прямым внутренним углом, — тоже прямой, поэтому каждый из остальных внутренних углов — острый.
Следствие 3. Из точки, взятой вне прямой, можно провести к этой прямой только один перпендикуляр, так как, предположив, что из взятой точки проходит и второй перпендикуляр к данной прямой, мы получили бы треугольник, внешний угол которого равняется внутреннему углу, не смежному с ним, что противоречит доказанной теореме.