Сумма внутренних углов треугольника
Теорема. Сумма внутренних углов треугольника равна двум прямым углам.
Возьмём какой-нибудь треугольник AВС (рис. 208). Обозначим его внутренние углы цифрами 1, 2 и 3. Докажем, что
∠1 + ∠2 + ∠3 = 180°.
Проведём через какую-нибудь вершину треугольника, например В, прямую МN параллельно АС.
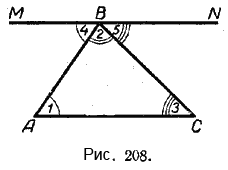
При вершине В мы получили три угла: ∠4, ∠2 и ∠5. Их сумма составляет развёрнутый угол, следовательно, она равна 180°:
∠4 + ∠2 + ∠5 = 180°.
Но ∠4 = ∠1 — это внутренние накрест лежащие углы при параллельных прямых МN и АС и секущей АВ.
∠5 = ∠3 — это внутренние накрест лежащие углы при параллельных прямых МN и АС и секущей ВС.
Значит, ∠4 и ∠5 можно заменить равными им ∠1 и ∠3.
Следовательно, ∠1 + ∠2 + ∠3 = 180°. Теорема доказана.
2. Свойство внешнего угла треугольника.
Теорема. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.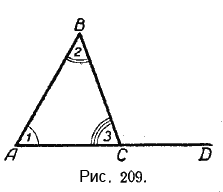
В самом деле, в треугольнике ABC (рис. 209) ∠1 + ∠2 = 180° — ∠3, но и ∠ВСD, внешний угол этого треугольника, не смежный с ∠1 и ∠2, также равен 180° — ∠3.
Таким образом:
∠1 + ∠2 = 180° — ∠3;
∠BCD = 180° — ∠3.
Следовательно, ∠1 + ∠2= ∠BCD.
Выведенное свойство внешнего угла треугольника уточняет содержание ранее доказанной теоремы о внешнем угле треугольника, в которой утверждалось только, что внешний угол треугольника больше каждого внутреннего угла треугольника, не смежного с ним; теперь же устанавливается, что внешний угол равен сумме обоих внутренних углов, не смежных с ним.
3. Свойство прямоугольного треугольника с углом в 30°.
Теорема. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.Пусть в прямоугольном треугольнике АСВ угол В равен 30° (рис. 210). Тогда другой его острый угол будет равен 60°.
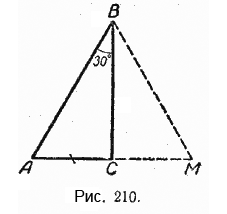
Докажем, что катет АС равен половине гипотенузы АВ. Продолжим катет АС за вершину прямого угла С и отложим отрезок СМ, равный отрезку АС. Точку М соединим с точкой В. Полученный треугольник ВСМ равен треугольнику АСВ. Мы видим, что каждый угол треугольника АВМ равен 60°, следовательно, этот треугольник — равносторонний.
Катет АС равен половине АМ, а так как АМ равняется АВ, то катет АС будет равен половине гипотенузы АВ.