Вписанные и описанные окружности: треугольник

Теорема 1. Около всякого треугольника можно описать окружность.

Описать окружность около треугольника — это значит построить такую окружность, которая проходила бы через его вершины, т. е. через три точки, не лежащие на одной прямой.

При решении задачи: «Через три точки, не лежащие на одной прямой, провести окружность» было установлено, что задача всегда имеет решение, и только одно.

На этом основании можем утверждать, что около любого треугольника можно описать окружность, и притом только одну.

Центром окружности, описанной около треугольника, является точка пересечения перпендикуляров, восстановленных к сторонам треугольника из их середин.

Теорема 2. Во всякий треугольник можно вписать окружность.

Пусть дан \(\Delta\)ABC (рис. 411). Проведём биссектрисы двух углов треугольника, например угла А и угла В. Опустим из точки их пересечения О перпендикуляры на стороны треугольника ABC: ОМ ⊥ АС, OK ⊥ AB и OP ⊥ ВС.

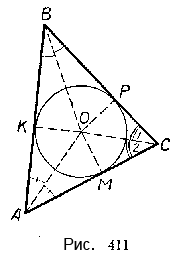
Все эти перпендикуляры равны между собой: ОР = О, К = ОМ

(так как ОР = ОК и ОМ = ОК, то и ОР = ОМ).

Следовательно, если из точки О как из центра радиусом, равным ОК, описать окружность, то прямые АВ, ВС и АС будут касательными к окружности О, так как они перпендикулярны к радиусам в конечной их точке на окружности.

Таким образом, окружность О будет вписанной в треугольник ABC.

Следствие. Все три биссектрисы треугольника пересекаются в одной точке.

В \(\Delta\)АВС (рис. 411) соединим центр окружности О с вершиной С треугольника и докажем, что ОС является биссектрисой ∠С.
Для этого сравним два прямоугольных треугольника: \(\Delta\)МОС и \(\Delta\)РОС. Они равны по гипотенузе (ОС) и катету (ОМ = ОР). Следовательно, ∠1 = ∠2, т. е. ОС является биссектрисой угла С. Таким образом, все три биссектрисы треугольника пересекаются в одной точке.