Построение треугольников. Признаки равенства треугольников.

Построение треугольников по одному или двум элементам

Пусть требуется построить треугольник по данной стороне а. Так как об углах треугольника и о других его сторонах ничего не сказано, то можем построить сколько угодно различных треугольников, у которых одна сторона будет равна отрезку а

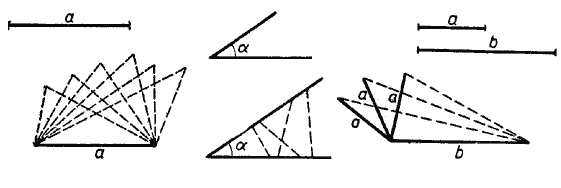
Пусть требуется построить треугольник по данному углу α. В этом случае также можно построить сколько угодно различных треугольников, имеющих данный угол,

Точно так же можно построить сколько угодно различных треугольников по двум сторонам, или по двум углам, или по углу и стороне (см. рис.).

Таким образом, если будут заданы только один или два элемента треугольника, то по этим элементам можно построить сколько угодно различных треугольников.

Далее о построении треугольников не по одному и не по двум, а по трём элементам:

1. Построение треугольника по двум данным его сторонам и углу между ними.
Первый признак равенства треугольников

Пусть требуется построить треугольник, одна сторона которого равна, например,

35 мм, другая сторона равна 32 мм и угол, заключённый между этими сторонами, равен 46°.

Построим с помощью транспортира ∠A, равный 46°, и на его сторонах отложим отрезки АВ и АС, соответственно равные 35 мм и 32 мм. Соединив точки В и С, получим искомый треугольник ABC.

По тем же данным построим другой треугольник - Δ А’В’С’.

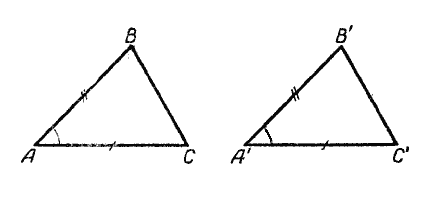
Докажем, что эти треугольники равны между собой.

Для этого наложим Δ А’В’С на Δ AВС так, чтобы вершины А’ и А совместились. Сторону А’С’ направим по стороне АС. Тогда точка С совместится с точкой С’, потому что А’С’ = АС.

Сторона А’В’ пойдёт по стороне АВ, так как ∠A’ = ∠A. Точка В’ совместится с точкой В, так как А’В’ = АВ. Если точки С и С’, В и В’ совместились, то совместятся и стороны В’С’ и ВС.

Треугольники ABC и А’В’С’ совпали, значит, они равны.

Мы можем по этим же данным построить сколько угодно треугольников, и все они будут равны между собой.

Таким образом, если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны между собой.

Назовём это первым признаком равенства треугольников.

Построение треугольника по стороне и двум прилежащим к ней углам.
Второй признак равенства треугольников

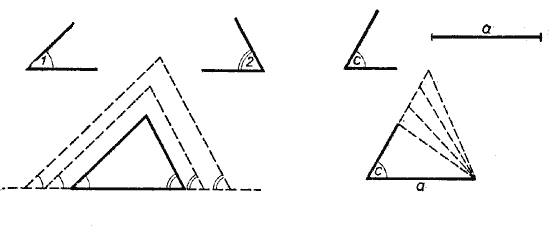
Пусть требуется построить треугольник, одна сторона которого равна, например, 40 мм, а углы, прилежащие к ней, равны 50° и 48°.

На произвольной прямой построим отрезок АС, равный 40 мм. Затем на этом отрезке при точке А построим угол, равный 50°, а при точке С - угол, равный 48°.

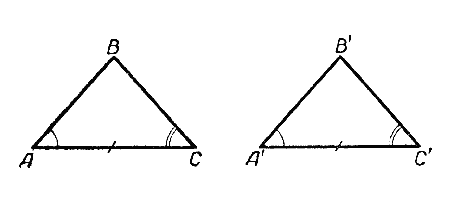
Если мы достаточно продолжим стороны этих углов, то они пересекутся в некоторой точке В. Получим треугольник ABC.

По тем же данным построим другой треугольник - Δ А’В’С’ и докажем, что эти треугольники будут равны между собой.

Для этого наложим Δ А’В’С’ на Δ ABC так, чтобы совместились равные стороны АС и А’С’. Тогда сторона А’В’ пойдёт по стороне АВ, так как ∠A’ = ∠A, и сторона С’В’ пойдёт по стороне СВ, так как ∠C’ = ∠C. Точка В’ одновременно должна быть и на стороне АВ, и на стороне СВ, следовательно, она совместится с точкой В, так как две прямые могут пересечься только в одной точке.

Треугольники ABC и А’В’С’ совпали, значит, они равные. По этим же данным можно построить сколько угодно треугольников, и все они будут равны между собой.

Таким образом, если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны между собой.

Назовём это вторым признаком равенства треугольников.

Построение треугольника по трём данным его сторонам.
Третий признак равенства треугольников

Пусть требуется построить треугольник по трём его сторонам, например, сторона а = 30 мм, сторона с = 40 мм и сторона b = 42 мм. (Заданные размеры должны удовлетворять условию: сумма двух любых сторон треугольника больше третьей стороны.)

Сначала на произвольной прямой построим отрезок АС, равный данному отрезку b, т. е. 42 мм; мы сразу получим две вершины искомого треугольника - А и С.

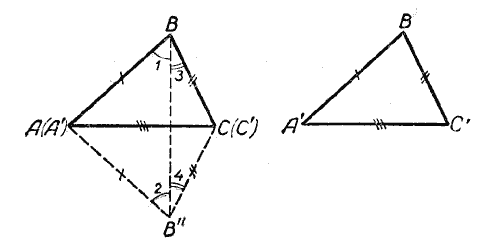
Так как длина второй и третьей сторон соответственно равна отрезкам с и а (в данном случае 40 мм и 30 мм), то третья вершина треугольника должна находиться как на дуге, описанной из центра А радиусом, равным 40 мм, так и на дуге, описанной из центра С радиусом, равным 30 мм. Следовательно, третьей вершиной треугольника будет точка пересечения этих дуг. Обозначив эту точку буквой В и соединив её отрезками с точками А и С, получим искомый треугольник ABC.

По тем же данным построим второй треугольник - Δ А’В’С’ и докажем,

что Δ АВС = Δ А’В’С’. Для этого приложим треугольник А’В’С’ к треугольнику ABC так, чтобы их равные стороны А’С’ и AС совместились, причём точка А’ совпала бы с точкой А, точка С - с точкой С. Тогда треугольник А’В’С’ примет положение АВ"С. Сторона АВ будет равна стороне АВ" и сторона ВС - стороне В"С.

Соединив отрезком прямой точки В и В", получим два равнобедренных треугольника ВАВ" и ВСВ", у которых ∠1 = ∠2, а ∠3 = ∠4, откуда ∠B = ∠B".

Следовательно, Δ АВС = Δ АВ"С, но тогда и Δ АВС = Δ А’В’С’.

По этим же данным можно построить сколько угодно треугольников, и все они будут равны между собой.

Мы доказали, что если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны между собой.

Назовём это третьим признаком равенства треугольников.

Замечания. 1. Во всех трёх признаках равенства треугольников в число трёх данных элементов входит хотя бы одна сторона треугольника.

2. В равных треугольниках против равных сторон лежат равные углы и, обратно, против равных углов лежат равные стороны.

Итак, три признака равенства треугольников:

1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны между собой

2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны между собой

3. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны между собой