Свойства медиан треугольника

Теорема. Все три медианы треугольника пересекаются в одной точке.

Пусть в треугольнике АBС (черт. 256) АD и ВЕ - медианы, пересекающиеся в точке О. Докажем, что и отрезок NС, проходящий через третью вершину этого треугольника и точку О, будет также медианой, т. е. AN = NВ.

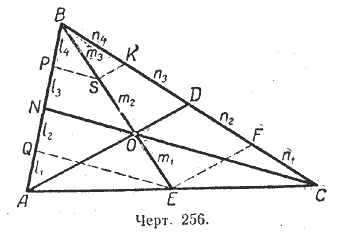
Для доказательства через точку Е проведём ЕF || АD, тогда СF = FD. Разделим отрезок ВD пополам; пусть DК = КВ. Получим n₁ =n₂ = n₃ = n₄, как половины равных отрезков СD и ВD.

Через точку K проведём KS || АD; тогда m₁ =m₂ = m₃, так как KS || ОD || ЕF и
n₄ =n₃ = n₂ .

Через точки Sи Е проведём SP || ОN и EQ || ОN, тогда l₄ =l₃ = l₂, так как SР || ОN || ЕQ и m₃ =m₂ = m₁. Кроме того, l₂ = l₁, так как AE = ЕС и ЕQ || СN.

Отсюда l₄ =l₃ = l₂ = l₁, но l₄ +l₃ = NВ, а l₂+ l₁ = NA.

Следовательно, AN = NВ, т. е. NС является так же медианой треугольника AВС.

Таким образом, все три медианы треугольника пересекаются в одной точке.

Кроме того, мы видим (черт. 256), что отрезок ОЕ составляет ¹/₃ВЕ. Аналогично можно доказать, что отрезок ON составляет ¹/₃ СN и отрезок ОD составляет ¹/₃ АD. Таким образом, точка пересечения медиан в треугольнике отделяет от каждой медианы третью часть, считая от соответствующей стороны.