Теорема Пифагора

Пифагор - греческий учёный, живший около 2500 лет назад (564-473 гг. до нашей эры).

Пусть дан прямоугольный треугольник, стороны которого а, b и с (рис. 267).

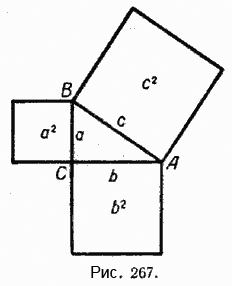
Построим на его сторонах квадраты. Площадиэтих квадратов соответственно равны а², b²и с². Докажем, что с² = а² + b².

Построим два квадрата МКОР и М’К’О’Р’ (рис. 268, 269), приняв за сторону каждого из них отрезок, равный сумме катетов прямоугольного треугольника АBС.

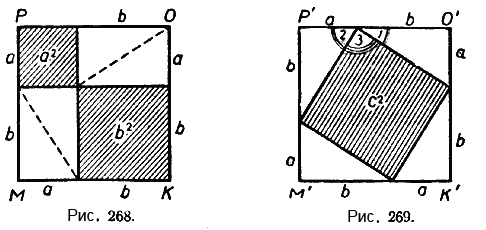
Выполнив в этих квадратах построения, показанные на риунках 268 и 269, мы увидим, что квадрат МКОР разбился на два квадрата с площадями а²и b²и четыре равных прямоугольных треугольника, каждый изкоторых равен прямоугольному треугольнику АВС. Квадрат М’К’О’Р’ разбился на четырёхугольник (он на рисунке 269 заштрихован) и четыре прямоугольных треугольника, каждый из которых также равен треугольнику АBС. Заштрихованный четырёхугольник - квадрат, так как стороны его равны (каждая равна гипотенузе треугольника АBС, т. е. с), а углы - прямые ∠1 + ∠2 = 90°, откуда ∠3 = 90°).

Таким образом, сумма площадей квадратов, построенных на катетах (на рисунке 268 эти квадраты заштрихованы), равна площади квадрата МКОР без суммы площадей четырёх равных треугольников, а площадь квадрата, построенного на гипотенузе (на рисунке 269 этот квадрат тоже заштрихован), равна площади квадрата М’К’О’Р’, равного квадрату МКОР, без суммы площадей четырёх таких же треугольников. Следовательно, площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах.

Получаем формулу с² = а² + b², где с - гипотенуза, а и b - катеты прямоугольного треугольника.

Теорему Пифагора кратко принято формулировать так:

Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.

Из формулы с² = а² + b²можно получить такие формулы:

а²= с² - b²;

b² = с² - а².

Этими формулами можно пользоваться для нахождения неизвестной стороны прямоугольного треугольника по двум данным его сторонам.

Например:

а) если даны катеты а = 4 см, b = 3 см, то можно найти гипотенузу (с):

с² = а² + b², т. е. с² = 4² + 3²; с² = 25, откуда с = √25 = 5(см);

б) если даны гипотенуза с = 17 см и катет а = 8 см, то можно найти другой катет (b):

b²= с² - а², т. е. b² = 17² - 8²; b² = 225, откуда b = √225 = 15 (см).

Следствие: Если в двух прямоугольных треугольниках ABC и А₁В₁С₁ гипотенузы с и с₁ равны, а катет b треугольника АBС больше катета b₁ треугольника А₁В₁C₁,

то катет а треугольника ABC меньше катета а₁ треугольника А₁В₁C₁.

В самом деле, на основании теоремы Пифагора получим:

а²= с²- b² ,

а₁²= с₁²- b₁²

В записанных формулах уменьшаемые равны, а вычитаемое в первой формуле больше вычитаемого во второй формуле, следовательно, первая разность меньше второй,

т. е. а² < а₁². Откуда а < а₁.