Свойство биссектрисы внутреннего угла треугольника

Теорема. Биссектриса любого угла треугольника (ABC) делит противоположную сторону на части (AD и CD), пропорциональные прилежащим сторонам треугольника.

Требуется доказать, что если ∠ABD = ∠DBC, то AD : DC = АВ : ВС.

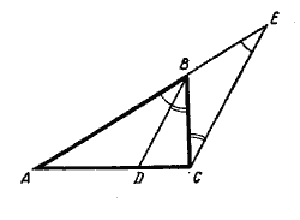
Проведём СЕ || BD до пересечения в точке Е с продолжением стороны АВ. Тогда, согласно теореме о пропорциональности отрезков, образующихся на прямых, пересечённых несколькими параллельными прямыми, будем иметь пропорцию:

AD : DC = АВ : BE.

Чтобы от этой пропорции перейти к той, которую требуется доказать, достаточно обнаружить, что ВЕ = ВС, т. е. что \(\Delta\)ВСЕ равнобедренный.

В этом треугольнике ∠Е = ∠ABD (как углы соответственные при параллельных прямых) и ∠ВСЕ = ∠DBC (как углы накрест лежащие при тех же параллельных прямых).

Но ∠ABD = ∠DBC по условию; значит, ∠Е = ∠ВСЕ, а потому равны и стороны BE и ВС, лежащие против равных углов.

Теперь, заменив в написанной выше пропорции BE на ВС, получим ту пропорцию, которую требуется доказать.

Пример. Пусть АВ = 10; ВС = 7 и АС = 6. Тогда, обозначив AD буквой x, можем написать пропорцию: x : (6 — x) = 10 : 7,

отсюда найдём:

7x = 60 — 10x; 7x + 10x = 60; 17x = 60;

x = ⁶⁰/₁₇ = 3 ⁹/₁₇

Следовательно,

DC = 6 — х = 6 — 3 ⁹/₁₇ = 2 ⁸/₁₇