Соотношения между сторонами и углами треугольника
Теорема 1. Против большей стороны в треугольнике лежит и больший угол.
Пусть в ΔАВС сторона АВ больше стороны ВС. Докажем, что угол С, лежащий против большей стороны АВ, больше угла А, лежащего против меньшей стороны ВС (рис.).
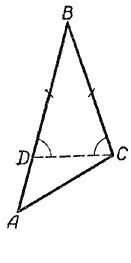
Отложим на стороне АВ от точки В отрезок ВD, равный стороне ВС, и соединим отрезком , точки D и С.
Треугольник DВС равнобедренный. Угол ВDС равен углу ВСD, так как они лежат против равных сторон в треугольнике.
Угол ВDС - внешний угол треугольника АDС, поэтому он больше угла А.
Так как ∠ВСD = ∠ВDС, то и угол ВСD больше угла А: ∠ВСD > ∠A. Но угол ВСD составляет только часть всего угла С, поэтому угол С будет и подавно больше угла A.
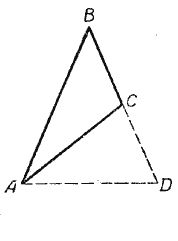
Теорема 2. Против равных углов в треугольнике лежат и равные стороны.
Пусть в Δ AВС ∠A = ∠С (рис.). Докажем, что AВ = ВС, т. е. треугольник АBС равнобедренный.
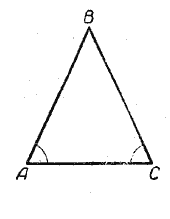
Между сторонами АВ и ВС может быть только одно из трёх следующих соотношений:
1) АВ > ВС;
2) АВ < ВС;
3) АВ = ВС.
Если бы сторона AВ была больше ВС, то угол С был бы больше угла A, но это противоречит условию теоремы, следовательно, АВ не может быть больше ВС.
Точно так же АВ не может быть меньше ВС, так как в этом случае угол С был бы меньше угла A.
Следовательно, возможен только третий случай, т. е.
АВ = ВС
Итaк, мы доказали: против равных углов в треугольнике лежат и равные стороны.
Теорема 3. Против большего угла в треугольнике лежит большая сторона.
Пусть в треугольнике АВС (рис.) ∠ C >∠ B
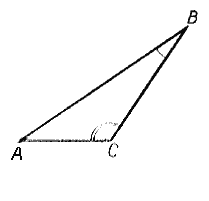
Докажем, что АВ > АС.
Здесь также может быть одно из трёх следующих соотношений:
1) АВ = АС;
2) АВ < АС;
3) АВ > АС.
Если бы сторона АВ была равна стороне АС, то ∠ С был бы равен ∠ В. Но это противоречит условию теоремы. Значит, АВ не может равняться АС
Точно так же АВ не может быть меньше АС, так как в этом случае угол С был бы меньше угла B, что также противоречит данному условию.
Следовательно, возможен только один случай, а именно:
АВ > АС.
Мы доказали: против большего угла в треугольнике лежит и большая сторона.
Следствие. В прямоугольном треугольнике гипотенуза больше любого из его катетов.
Соотношения между сторонами и углами в прямоугольном треугольнике
Пусть дан прямоугольный треугольник ABC. Обозначим его стороны через а, b и с.
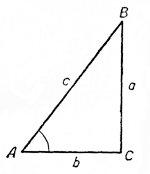
По определению тригонометрических функций:
a/c = sin ∠А; a/c = cos ∠В; b/c= sin ∠ В; b/c = cos ∠А.
Отсюда а = с sin ∠ А = с cos ∠В; b = c sin ∠B = с соs ∠A,
т. е. катет прямоугольного треугольника равен гипотенузе, умноженной на синус угла, противолежащего этому катету, или на косинус угла, прилежащего к нему.
Из того же прямоугольного треугольника имеем, что
a/b = tg ∠А , отсюда a = b tg ∠А;
b/a = ctg ∠А, откуда b = a ctg ∠А,
т.е. катет прямоугольного треугольника равен другому катету, умноженному на тангенс угла, противолежащего первому катету, или на котангенс угла, прилежащего к первому катету.