Тригонометрические соотношения в прямоугольном треугольнике
Возьмём прямоугольный треугольник ABC и обозначим его стороны буквами a, b и с. Рассмотрим сначала функции угла А.
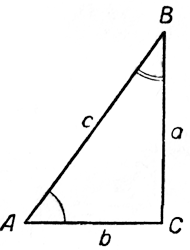
Отношение \( \frac{a}{c} \) называется синусом угла А,
т. е. синусом угла А называется отношение катета, противолежащего этому углу, к гипотенузе.
Отношение \( \frac{b}{c} \) называется косинусом угла А,
т. е. косинусом угла А называется отношение катета, прилежащего к этому углу, к гипотенузе.
Отношение \( \frac{a}{b} \) называется тангенсом угла А,
т. е. тангенсом угла А называется отношение катета, противолежащего этому углу, к катету прилежащему.
Отношение \( \frac{b}{a} \) называется котангенсом угла А,
т.е. котангенсом угла А называется отношение катета, прилежащего к этому углу, к катету противолежащему.
Отношение \( \frac{c}{b} \) называется секансом угла А.
Отношение \( \frac{c}{a} \) называется косекансом угла А.
Наиболее употребительными являются первые четыре функции: синус, косинус, тангенс и котангенс.
Эти функции угла A обозначаются так: sin ∠A, cos ∠A, tg ∠A и ctg ∠A;
$$ \frac{a}{c}=sinA; \frac{b}{c}=cosA; \frac{a}{b}=tgA; \frac{b}{a}=ctgA; $$Установим теперь функции для ∠В:
| b c |
- синус угла В, |
b c |
= |
sin ∠B |
| a c |
- косинус угла В, |
a c |
= |
cos ∠B |
| b a |
- тангенс угла В, |
b a |
= |
tg ∠B |
| a b |
- котангенс угла В |
a b |
= |
ctg ∠B |