Значения тригонометрических функций основных углов
Найдём значения тригонометрических функций для углов в 30°, 45° и 60°.
1) Для угла в 30°
Возьмём прямоугольный треугольник с острым углом в 30°. Обозначим длину гипотенузы АВ через с и выразим длины катетов.
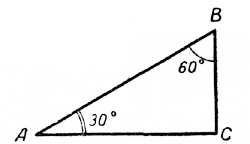
ВС = с/2, как катет, лежащий против угла в 30°.
Катет АС найдём по теореме Пифагора.
$$ AC = \sqrt{AB^2 - BC^2} = \sqrt{c^2 - \frac{c^2}{4}} = \sqrt{\frac{3c^2}{4}} = \frac{c\sqrt3}{2} $$Тогда
sin30o = \( \frac{BC}{AB}=\frac{\frac{c}{2}}{c}=\frac{1}{2}=0,5 \)
tg30o = \( \frac{BC}{AC}=\frac{\frac{c}{2}}{\frac{c\sqrt3}{2}}=\frac{1}{\sqrt3}=\frac{\sqrt3}{3}\approx 0,5774 \)
cos30o= \( \frac{AC}{AB}=\frac{\frac{c\sqrt3}{2}}{c}=\frac{\sqrt3}{2}\approx 0,8660 \)
2) Для угла в 45°.
Возьмём прямоугольный треугольник с острыми углами по 45°.
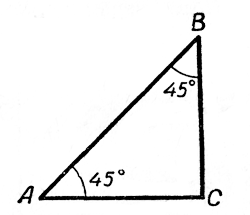
Обозначим длину гипотенузы AB через c и выразим длины катетов. АС = BC, следовательно, по теореме Пифагора
AB2 = 2BC2, откуда
$$ BC^2 = \frac{AB^2}{2} = \frac{2AB^2}{4} = \frac{2c^2}{4} $$
Значит, \(BC = \sqrt{\frac{2c^2}{4}} = \frac{c\sqrt2}{2}\), одновременно и \(AC = \frac{c\sqrt2}{2}\)
sin 45° = \( \frac{BC}{AB} = \frac{\frac{c\sqrt2}{2}}{c} = \frac{\sqrt2}{2} \approx 0,7071 \)
tg 45°= \( \frac{BC}{AC} = 1 \)
cos 45°= \( \frac{BC}{AB} = \frac{\sqrt2}{2} \approx 0,7071 \)
3) Для угла в 60°
Значения тригонометрических функций для угла в 60° можно найти из того же треугольника, из которого нашли значения тригонометрических функций для угла в 30°, так как если ∠A = 30°, то ∠В = 60°.
Тогда
sin 60° = \( \frac{AC}{AB} = \frac{\sqrt3}{2} \approx 0,8660 \)
tg 60° = \( \frac{AC}{BC} = \sqrt3 \approx 1,7321 \)
cos 60° = \( \frac{BC}{AB} = \frac{1}{2} = 0,5\)
Таблица значений тригонометрических функций для углов в 30°, 45° и 60°.
|
УГОЛ |
СИНУС |
КОСИНУС |
ТАНГЕНС |
|
30о |
\( \frac{1}{2}=0,5 \) |
\( \frac{\sqrt3}{2}\approx 0,8660 \) |
\( \frac{\sqrt3}{3}\approx 0,5774 \) |
|
45о |
\( \frac{\sqrt2}{2}\approx 0,7071 \) |
\( \frac{\sqrt2}{2}\approx 0,7071 \) |
1 |
|
60о |
\( \frac{\sqrt3}{2}\approx 0,8660 \) |
\( \frac{1}{2}=0,5 \) |
\( \sqrt3 \approx 1,7321 \) |
Рассматривая эту таблицу, можно заметить, что синус и тангенс острого угла возрастают при увеличении угла, а косинус при увеличении угла убывает.
При уменьшении угла синус и тангенс убывают, а кoсинус возрастает.
Тригонометрические функции дополнительных углов
Дополнительными углами называются два угла, которые в сумме составляют 90°. Такими углами, в частности, являются острые углы прямоугольного треугольника.
Углы А и В в прямоугольном треугольнике ACB являются дополнительными углами, так как
∠A + ∠B = 90°; ∠A = 90° - ∠B; ∠В = 90° - ∠A
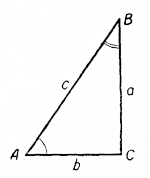
Рассмотрим соотношения между тригонометрическими функциями дополнительных углов.
1) \( sinA = \frac{a}{c}; cosB = \frac{a}{c} \), т. e. синус данного угла равен косинусу дополнительного угла.
2) \( cosA = \frac{b}{c}; sinB = \frac{b}{c} \), т.е. косинус данного угла равен синусу дополнительного угла.
3) \( tgA = \frac{a}{b}; ctgB = \frac{a}{b} \), т.е. тангенс данного угла равен котангенсу дополнительного угла.
4) \( ctgA = \frac{b}{a}; tgB = \frac{b}{a} \), т.e. котангенс данного угла равен тангенсу дополнительного угла.
Знание соотношений между тригонометрическими функциями дополнительных углов важно для понимания устройства тригонометрических таблиц.