Теорема синусов. Теорема косинусов

При решении прямоугольных треугольников используются только основные тригонометрические функции. Для решения же косоугольных треугольников потребуется знание зависимостей между сторонами и тригонометрическими функциями углов косоугольных треугольников, известные как теоремы синусов, косинусов и тангенсов. К выводу этих теорем мы и переходим.

В дальнейшем мы будем пользоваться следующими обозначениями: a, b и c - стороны треугольника; А, В и С - противолежащие им углы; S - площадь; 2р - периметр; R - радиус описанного круга; r - радиус вписанного круга; h_а, l_а и m_а - высота, биссектриса и медиана, соответствующие стороне а.

Теорема синусов

Теорема. Во всяком треугольнике стороны пропорциональны синусам противолежащих углов:

$$ \frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} $$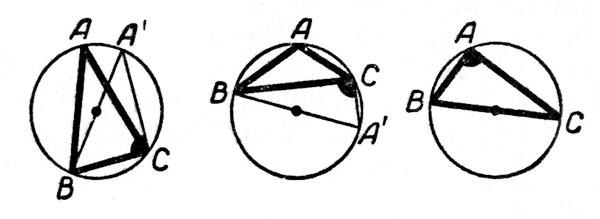

Доказательство. Опишем круг около данного треугольника ABC. Пусть R - радиус этого круга. Возьмём одну из вершин треугольника, например А; через одну из других вершин, например через В, проведём диаметр ВА’ описанного круга. Вспомогательный треугольник А’ВС прямоугольный, так как вписанный угол А’СВ опирается на диаметр. Из вспомогательного треугольника найдём:

а = 2Rsin A’.

Если угол А острый, то А = А’, так как вписанные углы A и A’ опираются на одну и ту же дугу.
Если угол А тупой, то угол А’ острый, измеряющийся половиной дуги ВАС:

$$ A’ = \frac{1}{2}\smile BAC = \frac{1}{2}(2\pi-\smile BA’C) = \pi - \frac{\smile BA’C}{2} = \pi-A $$

Итак, или A= А’, или A’ =\(\pi\) - A, в обоих случаях sin A’ = sin A, а потому

а = 2R sin A. (1)

Если угол Aпрямой, то а = 2R, sin A= 1 и равенство (1) также справедливо.

Аналогичные равенства найдём и для прочих углов В и С. Итак,

а =2R sin A; b =2R sin В; с = 2R sin С, откуда

$$ \frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2R $$

Следствие. Отношение стороны треугольника к синусу противолежащего угла равно диаметру круга, описанного около треугольника.

Теорема косинусов

Теорема. Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:

а² =b² + с² - 2bccosА

b² =c² + a² - 2cacosB

c² =a² + b² - 2abcosC

Доказательство. Докажем первое равенство.

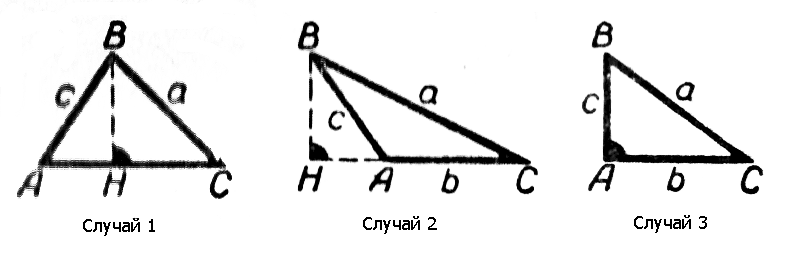
Случай 1. Угол A острый.

Пусть ВН - высота, опущенная из вершины В ; из геометрии известно, что
а² = b² + с²-2b · АН. (1)
Из прямоугольного треугольника АВН найдём
АН = с cos А; подставив в формулу (1), получим доказываемое равенство.

Случай 2. Угол A тупой.
В этом случае а² = b² + с² +2b · АН. (2)

Из треугольника АВН найдём:
АН = с cos∠BAH = с cos(\(\pi\) - A) = - с cosA.

Подставив в формулу (2), получим доказываемое равенство.

Случай 3. Угол А прямой.

В этом случае (по теореме Пифагора):

а² = b² + с²= b² + с² - 2bccosА

(так как cos А = 0).

Итак, во всех случаях

а² = b² + с² - 2bccosА