Основные соотношения между тригонометрическими функциями одного аргумента

Прежде всего отметим уже известные нам тождества

$$ tg \phi=\frac{sin \phi}{cos \phi} \;\;(1)$$
$$ ctg \phi=\frac{cos \phi}{sin \phi} \;\;(2)$$

Из этих двух тождеств следует, что

tg φ • ctg φ = 1 (3)

Теперь покажем, что для любого угла φ

sin² φ + cos²φ = 1 (4)

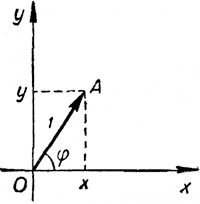
Предположим, что \(\overrightarrow{OA}\) = (х, у) есть вектор единичной длины, образующий с осью x угол φ. Тогда

cosφ=x

sinφ=y

Квадрат длины любого вектора равен сумме квадратов его координат. Из этого утверждения и вытекает формула (4).

Нам известны также следующие соотношения:

$$ sec \phi=\frac{1}{cos \phi} \;\;(5)$$
$$ cosec \phi=\frac{1}{sin \phi}\;\;(6)$$

К полученным шести тождествам добавим еще два:

1 + tg² φ = sec² φ, (7)

1 + ctg² φ = cosec² φ. (8)

Докажем, например, тождество (7):

$$ 1+tg^2\phi = 1+\frac{sin^2\phi}{cos^2\phi} = \frac{cos^2\phi + sin^2\phi}{cos^2\phi} =\\= \frac{1}{cos^2\phi}=sec^2\phi $$

Аналогично доказывается и тождество (8).