Построить угол по косинусу, синусу, тангенсу
Покажем на конкретных задачах , как строятся углы по известным значениям их тригонометрических функций.
Задача 1. Построить угол φ, синус которого равен а.
Если |а|>1, то построить такой угол нельзя, потому что он вообще не существует (синус любого угла по абсолютной величине не превышает единицы).
Если же |а|<1, то поступаем таким образом.
Проводим окружность радиуса 1 с центром в начале координат. На оси Оу отмечаем точку В с ординатой a и проводим через нее прямую, параллельную оси абсцисс.
Точки пересечения этой прямой с окружностью обозначим через A1 и A2.
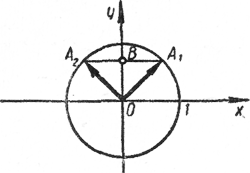
Векторы \(\overrightarrow{OA_1}\) и \(\overrightarrow{OA_2}\) имеют единичную длину, а их ординаты равны a. Поэтому все углы, для которых \(\overrightarrow{OA_1}\)и \(\overrightarrow{OA_2}\) являются конечными сторонами, имеют синус, равный a.
Замечание. Если а = 1, то описанным выше способом мы получаем не два, а только один вектор \(\overrightarrow{OB}\), образующий искомые углы с положительным направлением оси абсцисс. В этом случае φ = 90° + ... + 360°n. Аналогично обстоит дело и при а = -1 . В этом случае φ = -90° + 360°n.
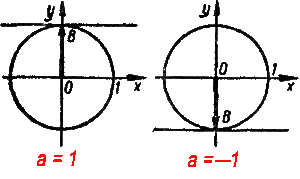
Задача 2. Построить угол φ, косинус которого равен а.
Как и в задаче 1, требуемое построение можно выполнить лишь при |а|<1.
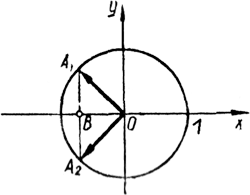
На оси Ох отмечаем точку В с абсциссой a и через нее проводим прямую, параллельную оси ординат (на рисунке число a отрицательно). Точки пересечения этой прямой с единичной окружностью обозначим через A1 и A2. Искомыми углами будут углы, для которых конечными сторонами являются \(\overrightarrow{OA_1}\) и \(\overrightarrow{OA_2}\).
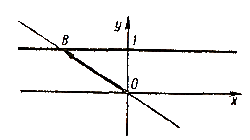
Задача 3. Построить угол φ, тангенс которого равен а.
На оси тангенсов отмечаем точку В с ординатой a . Все углы, конечные стороны которых лежат на прямой ОВ, имеют тангенс, равный a.
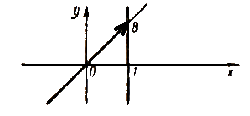
Задача 4. Построить угол φ, котангенс которого равен а.
На оси котангенсов отмечаем точку В с абсциссой a. Все углы, конечные стороны которых лежат на прямой ОВ, имеют котангенс, равный a.