Решение тригонометрических уравнений графически
Уравнения, с которыми приходится сталкиваться при решении практических задач, как правило, значительно отличаются от тех, которые мы рассматривали. Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Современная математика располагает эффективными методами приближенного решения уравнений. Рассмотрим графический способ решения.
Пусть, например, нужно решить уравнение
sin х = 1 - х.
На одном и том же рисунке начертим два графика: график функции y = sin х и график функции у = 1 - х
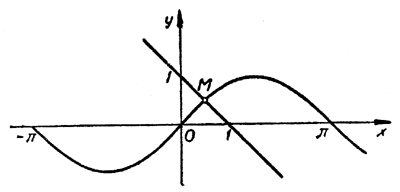
Эти графики пересекаются в одной точке М. Абсцисса этой точки и дает нам единственный корень нашего уравнения:
х ≈ 0,5.
Для уточнения полученного результата полезно использовать тригонометрические таблицы или компьютерные программы. При х = 0,5
sin x ≈ 0,4794,
1 - х = 0,5;
следовательно, sin х < 1 - х. Но тогда, как легко понять из рисунка, корень уравнения sin х = 1 - х будет больше, чем 0,5. Проверим значение х = 0,6. Имеем (при х = 0,6):
sin х ≈ 0,5446,
1 - х = 0,4;
следовательно, sin х > 1 - х. Но тогда, как легко понять из того же рисунка, искомый корень x0 должен быть меньше, чем 0,6. Теперь уже мы знаем, что x0 находится в интервале [0,5; 0,6]. Поэтому с точностью до 0,1
x0 ≈0,5 (с недостатком),
x0 ≈ 0,6 (с избытком).
С помощью таблиц можно найти приближенное значение x0 и с точностью до 0,01. Разделим интервал [0,5; 0,6] пополам. В средней точке (x = 0,55) этого интервала
sin х ≈ 0,5227,
1 - х = 0,45.
Опять получаем, что sin х > 1 - х. Следовательно, x0 < 0,55.
Проверим точку х = 0,52 (она близка к средней точке х = 0,525 интервала [0,50; 0,55], в котором заключен корень x0). При х = 0,52
sin х ≈ 0,4969,
1 - х = 0,48.
Снова sin x > 1 - х; поэтому x0 < 0,52. Итак, 0,50 < x0 < 0,52. Поэтому с точностью до 0,01
x0 ≈ 0,51.
Для примера рассмотрим уравнение
tg x/2 = 2 - x.
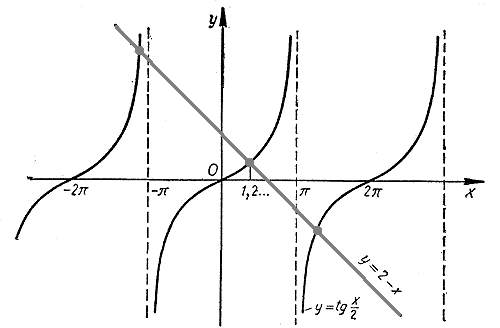
Графики функций у = tg x/2 и у = 2 - х пересекаются в бесконечном числе точек. Значит, данное уравнение имеет бесконечное множество корней. Найдем, например, наименьший положительный корень х0. Этот корень является абсциссой точки пересечения графиков. Примерно он равен 1,2.
Чтобы найти этот корень точнее, воспользуемся таблицами тангенсов В. М. Брадиса (или рассчитаем соответствующие значения в программе "Kалькулятор" или "Excel"). Выпишем значения функций у = tg x/2 и у = 2 - х в окрестности точки х = 1,2.
| x | 1,2 | 1,3 |
| y=tg x/2 | 0,6841 | 0,7602 |
| y=2-x | 0,8000 | 0,7000 |
| tg x/2-(2-x) | -0,1159 | 0,0602 |
Как видно из этой таблицы, при переходе от значения х = 1,2 к значению х = 1,3 разность tg x/2 - (2 - х) меняет свой знак на противоположный (с - на +). Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х0 ≈ 1,2 (с недостатком) или х0 ≈ 1,3 (с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня
с точностью до 0,01. Для этого рассмотрим значение х = 1,25, являющееся средним значением чисел 1,2 и 1,3. При х = 1,25
tg x/2 ≈ 0,7215,
2 - х = 0,7500.
Поскольку tg x/2 < 2- х, то х0 >1,25. Итак,
1,25< х0 < 1,30.
Теперь испытаем значение х = 1,28, которое близко к среднему значению чисел 1,25 и 1,30. При х = 1,28
tg x/2 ≈ 0,7445,
2 - х = 0,7200.
Теперь уже tg x/2 >2 - х Значит , х0 < 1,28.
Аналогично, рассматривая значение х = 1,26, мы получили бы tg x/2 < 2 - х и потому х0 > 1,26. Значит,
1,26 <х0< 1,28.
Поэтому с точностью до 0,01
х0 ≈ 1,27
Если бы нужно было определить, какое это приближенное значение (с недостатком или с избытком), то пришлось бы сравнить значения tg x/2 и 2 - х в точке х = 1,27.