Равенство прямоугольных треугольников
1. Первые два признака равенства прямоугольных треугольников.
Для равенства двух треугольников достаточно, чтобы три элемента одного треугольника были равны соответствующим элементам другого треугольника, при этом непременно в число этих элементов должна входить хотя бы одна сторона.
Так как все прямые углы равны между собой, то прямоугольные треугольники уже имеют по одному равному элементу, именно по одному прямому углу.
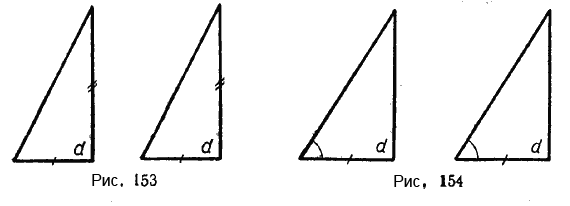
Отсюда следует, что прямоугольные треугольники равны:
если катеты одного треугольника соответственно равны катетам другого треугольника (рис. 153);
если катет и прилежащий острый угол одного угольника соответственно равны катету и прилежащему острому углу другого треугольника (рис. 154).
Докажем теперь две теоремы, устанавливающие ещё два признака равенства прямоугольных треугольников.
Теоремы о признаках равенства прямоугольных треугольников
Теорема 1. Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе иострому углу другого треугольника, то такие прямоугольные треугольники равны.Чтобы доказать эту теорему, построим два прямоугольных гольника ABC и А’В’С’, у которых углы А и А’ равны, гипотенузы АВ и А’В’ также равны, а углы С и С’ — прямые (рис. 157).
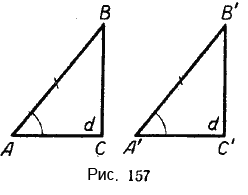
Наложим треугольник А’В’С’на треугольник ABC так, чтобы вершина А’ совпала с вершиной А, гипотенуза А’В’ — с равной гипотенузой АВ. Тогда вследствие равенства углов A и А’ катет А’С’ пойдёт по катету АС; катет В’С’ совместится с катетом ВС: оба они - перпендикуляры, проведённые к одной прямой АС из одной точки В. Значит, вершины С и С’ совместятся.
Треугольник ABC совместился с треугольником А’В’С’.
Следовательно, \(\Delta\)АВС = \(\Delta\)А’В’С’.
Эта теорема даёт 3-й признак равенства прямоугольных треугольников (по гипотенузе и острому углу).
Теорема 2. Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные треугольники равны.
Чтобы доказать это, построим два прямоугольных треугольника АВС и А’В’С’, у которых углы С и С’ — прямые, катеты АС и A’C’ равны, гипотенузы АВ и А’В’ также равны (рис. 158).
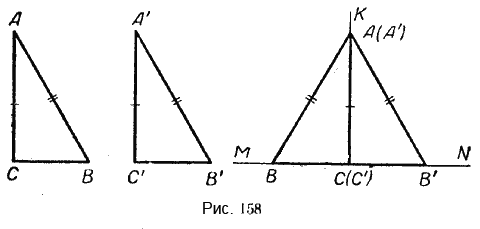
Проведём прямую MN и отметим на ней точку С, из этой точки проведём перпендикуляр СК к прямой MN. Затем прямой угол треугольника ABC наложим на прямой угол КСМ так, чтобы вершины их совместились и катет АС пошёл по лучу СК, тогда катет ВС пойдёт по лучу СМ. Прямой угол треугольника А’В’С’ наложим на прямой угол KCN так, чтобы вершины их совместились и катет А’С’ пошёл по лучу СК, тогда катет С’В’ пойдёт по лучу CN. Вершины А и А’ совпадут вследствие равенства катетов АС и А’С’.
Треугольники АВС и А’В’С’ составят вместе равнобедренный треугольник ВАВ’, в котором АС окажется высотой и биссектрисой, а значит и осью симметрии треугольника ВАВ’. Из этого следует, что \(\Delta\)АВС = \(\Delta\)А’В’С’.
Эта теорема дает 4-й признак равенства прямоугольных треугольников (по гипотенузе и катету).
Итак, все признаки равенства прямоугольных треугольников:
1. Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники равны
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны
3. Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны
4. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны
5. Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие прямоугольные треугольники равны