Средняя линия треугольника

Теорема. Отрезок,соединяющий середины двух сторон треугольника, параллелен третьей стороне треугольника и равен ее половине.

Дано: в треугольнике АВС АМ = ВМ и СК = ВК. Надо доказать:

1) МК || АС;

2) МК = ^AC/₂ .

Доказательство. Продолжим МК на отрезок КЕ = МК и точку С соединим с точкой Е.

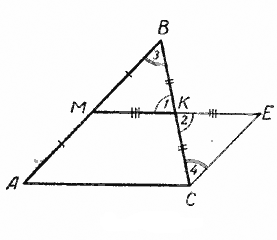
Рассмотрим треугольники МВК и КЕС.

СК = КВ — по условию,

КЕ = МК — по построению,

∠1 = ∠2, как вертикальные

Следовательно \(\Delta\) МВК = \(\Delta\)КЕС

Из равенства этих треугольников следует:

1) ЕС = МВ и, значит, ЕС = АМ;

2) ∠4 = ∠3, но это углы внутренние накрест лежащие при прямых ЕС и МВ и секущей ВС, следовательно, ЕС || МВ и, значит, ЕС || АМ.

Рассмотрим теперь четырёхугольник АМЕС. В нем ЕС = АМ и ЕС || АМ, поэтому

АМЕС — параллелограмм (см. тут).

Из этого cледует:

1) МЕ || АС и, значит, МК ||АС,

2) МЕ = AС и, значит, МК = ^AC/₂

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.