Метод введения вспомогательного угла

Преобразование выражения a sin х + b cos х путем введения вспомогательного угла

Лемма. Если сумма квадратов двух действительных чисел равна единице, то одно из этих чисел можно рассматривать как косинус, а другое как синус некоторого угла.

Другими словами, если а² + b² = 1, то существует угол φ, такой, что

а = cos φ; b = sin φ.

Прежде чем доказывать эту лемму, поясним ее на следующем примере:

$$ (\frac{\sqrt3}{2})^2 + (\frac{1}{2}) = \frac{3}{4} + \frac{1}{4} = 1 $$

Поэтому существует угол φ, такой, что \( \frac{\sqrt3}{2} \) = cos φ; ¹/₂ = sin φ.

В качестве φ в данном случае можно выбрать любой из углов 30°, 30° ± 360°, 30° ± 2 • 360° и т. д.

Доказательство леммы:

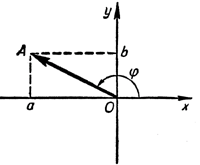
Рассмотрим вектор \(\vec{0А}\) с координатами (а, b). Поскольку а² + b² = 1, длина этого вектора равна 1. Но в таком случае его координаты должны быть равны cos φ и sin φ, где φ - угол, который образует данный вектор с осью абсцисс.

Итак, а = cos φ; b =sin φ, что и требовалось доказать.

Доказанная лемма позволяет преобразовать выражение a sin х + b cos х к более удобному для изучения виду.

Прежде всего вынесем за скобки выражение \(\sqrt{a^2 + b^2}\)

$$ a sinx + b cosx = \sqrt{a^2 + b^2}(\frac{a}{\sqrt{a^2 + b^2}}sinx + \frac{b}{\sqrt{a^2 + b^2}}cosx) $$

Поскольку

$$ (\frac{a}{\sqrt{a^2 + b^2}})^2 + (\frac{b}{\sqrt{a^2 + b^2}})^2 = 1 $$

первое из чисел \( \frac{a}{\sqrt{a^2 + b^2}} \) и \( \frac{b}{\sqrt{a^2 + b^2}} \) можно рассматривать как косинус некоторого угла φ, а второе - как синус того же угла φ:

$$ \frac{a}{\sqrt{a^2 + b^2}} = cos\phi, \;\; \frac{b}{\sqrt{a^2 + b^2}} = sin\phi $$

Но в таком случае

a sin х + b cos х = \(\sqrt{a^2 + b^2}\)(cos φ sin х + sin φ cos х) = \(\sqrt{a^2 + b^2}\) sin ( x + φ )

Итак,

a sin х + b cos х = \(\sqrt{a^2 + b^2}\) sin (x + φ) , где угол φ определяется из условий

$$ sin\phi = \frac{b}{\sqrt{a^2 + b^2}} \;\; cos\phi = \frac{a}{\sqrt{a^2 + b^2}} $$

Примеры.

1) \( sin x + cos x = \sqrt2 (\frac{1}{\sqrt2} sin x + \frac{1}{\sqrt2}cos x) = \sqrt2 (cos\frac{\pi}{4}sin x + sin\frac{\pi}{4}cos x ) =\\= \sqrt2(sinx + \frac{\pi}{4}) \)

Полученную формулу sin x + cos x = \(\sqrt2(sinx + \frac{\pi}{4})\)полезно запомнить.

2) Если одно из чисел а и b положительно, а другое отрицательно, то выражение
a sin х + b cos х удобнее преобразовывать не к синусу суммы, а к синусу разности двух углов. Так,

$$ 3sinx - 4cosx = \sqrt{9+16}(\frac{3}{\sqrt{9+16}}sinx - \frac{4}{\sqrt{9+16}}cosx) =\\= 5(sinx\cdot\frac{3}{5} - cosx\cdot\frac{4}{5}) = 5sin(x - \phi), $$

где под φ можно подразумевать любой угол, удовлетворяющий условиям:

cos φ = ³/₅ , sin φ = ⁴/₅

В частности, можно положить φ = arctg ⁴/₃. Тогда получим:

3 sin х - 4 cos x = 5 sin (x - arctg ⁴/₃).