Косинус суммы двух углов

Докажем следующие две формулы:

cos (α + β) = cos α cos β - sin α sin β, (1)

cos (α - β) = cos α cos β + sin α sin β. (2)

Косинус суммы (разности) двух углов равен произведению косинусов этих углов минус (плюс) произведение синусов этих углов.

Нам удобнее будет начать с доказательства формулы (2). Для простоты изложения предположим сначала, что углы α и β удовлетворяют следующим условиям:

1) каждый из этих углов неотрицателен и меньше 2π:

0 < α < 2π, 0 < β < 2π;

2) α > β .

Пусть положительная часть оси 0х является общей начальной стороной углов α и β.

Конечные стороны этих углов обозначим соответственно через 0А и 0В. Очевидно, что угол α - β можно рассматривать как такой угол, на который нужно повернуть луч 0В вокруг точки 0 против часовой стрелки, чтобы его направление совпало с направлением луча 0А.

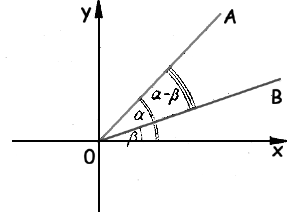
На лучах 0А и 0В отметим точки М и N, отстоящие от начала координат 0 на расстоянии 1, так что 0М = 0N = 1.

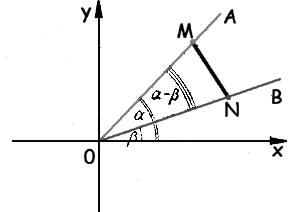
В системе координат х0у точка М имеет координаты (cos α, sin α), а точка N - координаты (cos β , sin β ). Поэтому квадрат расстояния между ними равен:

d₁² = (cos α - cos β)² + (sin α - sin β)² = cos² α - 2 cos α cos β +

+ cos²β + sin² α - 2sin α sin β + sin² β = 2 (1 - cos α cos β - sin α sin β).

При вычислениях мы воспользовались тождеством

sin² φ + cos² φ = 1.

Теперь рассмотрим другую систему координат В0С, которая получается путем поворота осей 0х и 0у вокруг точки 0 против часовой стрелки на угол β.

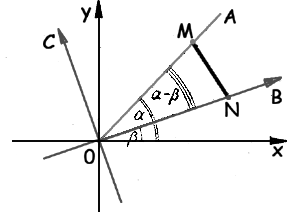
В этой системе координат точка М имеет координаты (cos (α - β), sin (α - β)), а точка N -координаты (1,0). Поэтому квадрат расстояния между ними равен:

d₂² = [cos (α - β) - 1] ² + [sin (α - β) - 0]² = cos² (α - β) - 2 cos (α - β) + 1 +

+ sin² (α - β) = 2 [1- cos(α - β)].

Но расстояние между точками М и N не зависит от того, относительно какой системы координат мы рассматриваем эти точки. Поэтому

d₁² = d₂²

или

2 (1 - cos α cos β - sin α sin β) = 2 [1- cos(α - β)].

Отсюда и вытекает формула (2).

Теперь следует вспомнить о тех двух ограничениях, которые мы наложили для простоты изложения на углы α и β.

Требование, чтобы каждый из углов α и β был неотрицательным, на самом деле не существенно. Ведь к любому из этих углов можно прибавить угол, кратный 2r, что никак не отразится на справедливости формулы (2). Точно так же от каждого из данных углов можно вычесть угол, кратный 2π . Поэтому можно считать, что 0 < α < 2π, 0 < β < 2π.

Не существенным оказывается и условие α > β. Действительно, если α < β, то β >α; поэтому, учитывая четность функции cos х, получаем:

cos (α - β) = cos (β - α) = cos β cos α + sin β sin α,

что по существу совпадает с формулой (2). Таким образом, формула

cos (α - β) = cos α cos β + sin α sin β

верна для любых углов α и β. В частности, заменяя в ней β на -β и учитывая, что функция cos х является четной, а функция sin х нечетной, получаем:

cos (α + β) = cos [α - ( - β)] =cos α cos (-β) + sin α sin (-β) =

= cos α cos β - sin α sin β,

что доказывает формулу (1).

Итак, формулы (1) и (2) доказаны.

Примеры.

1) cos 75° = cos (30° + 45°) = cos 30° • cos 45°-sin 30°-sin 45° =

\( \frac{\sqrt3}{2}\cdot\frac{\sqrt2}{2} - \frac{1}{2}\cdot\frac{\sqrt2}{2}=\frac{\sqrt6 - \sqrt2}{4} \)

2) cos 15° = cos (45° - 30°) = cos 45° • cos 30° + sin 45°• sin 30° =

\( \frac{\sqrt2}{2}\cdot\frac{\sqrt3}{2} + \frac{\sqrt2}{2}\cdot\frac{1}{2}=\frac{\sqrt6 + \sqrt2}{4} \)