Теорема тангенсов

Теорема. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов:

$$ \frac{a-b}{a+b} = \frac{tg\frac{A-B}{2}}{tg\frac{A+B}{2}} $$

(и две аналогичные формулы для прочих пар сторон а, с и b, с).

Доказательство. В силу теоремы синусов имеем:

$$ a - b = 2R(sinA - sinB) = 4Rcos{\frac{A+B}{2}}sin{\frac{A-B}{2}} $$
$$ a + b = 2R(sinA + sinB) = 4Rsin{\frac{A+B}{2}}cos{\frac{A-B}{2}} $$

Разделив почленно эти равенства, получим доказываемую формулу.

Тангенс суммы и разности двух углов

Формулы для выражения синуса и косинуса суммы (разности) двух углов через синусы и косинусы этих углов позволяют получить соответствующие формулы для тангенса и котангенса.

Действительно,

$$ tg(\alpha + \beta) = \frac{sin(\alpha + \beta)}{cos(\alpha + \beta)} =\\= \frac{sin\alpha\cdot cos\beta + sin\beta\cdot cos\alpha}{cos\alpha\cdot cos\beta - sin\alpha\cdot sin\beta} $$

Предположим, что cos α и cos β отличны от нуля (это равносильно тому, что tg α и tg β определены). Тогда, разделив числитель и знаменатель последней дроби на cos α • cos β, получим.

$$ \frac{sin\alpha\cdot cos\beta + sin\beta\cdot cos\alpha}{cos\alpha\cdot cos\beta - sin\alpha\cdot sin\beta} =\\=
\frac{\frac{sin\alpha cos\beta + sin\beta cos\alpha}{cos\alpha cos\beta}}{\frac{cos\alpha cos\beta - sin\alpha sin\beta}{cos\alpha cos\beta}} = \frac{tg\alpha + tg\beta}{1 - tg\alpha ig\beta} $$

Итак, если тангенсы углов α , β и α + β определены, то

$$ tg(\alpha + \beta) = \frac{tg\alpha + tg\beta}{1 - tg\alpha \cdot tg\beta} $$

Тангенс суммы двух углов равен сумме тангенсов этих углов, деленной на единицу минус произведение тангенсов этих углов.

Пример.

$$ tg(\frac{\pi}{4}+\alpha) = \frac{tg\frac{\pi}{4}+tg\alpha}{1-tg\frac{\pi}{4}\cdot tg\alpha} = \frac{1+tg\alpha}{1-tg\alpha} $$

Заменяя в формуле (1) β на (-β ) и учитывая, что функция у = tg х является нечетной, получаем:

$$ tg(\alpha - \beta)=\frac{tg\alpha + tg(-\beta)}{1-tg\alpha tg(-\beta)} = \frac{tg\alpha - tg\beta}{1+tg\alpha tg\beta}; $$

Тангенс разности двух углов равен разности тангенсов этих углов, деленной на единицу плюс произведение тангенсов этих углов.

Пример 1.

$$ tg(\frac{\pi}{4}-\alpha) = \frac{tg\frac{\pi}{4}-tg\alpha}{1+tg\frac{\pi}{4}\cdot tg\alpha} = \frac{1-tg\alpha}{1+tg\alpha} $$

Пример 2.

Пусть прямая у = k₁x образует с осью абсцисс угол α , а прямая у = k₂x - угол β

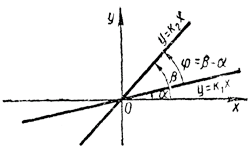
Тогда угол φ между этими прямыми будет равен φ = β - α .

Предположим, что рассматриваемые прямые не перпендикулярны друг другу. Тогда тангенс угла φ существует и равен

$$ tg\phi = tg(\beta - \alpha) = \frac{tg\beta - tg\alpha}{1+tg\beta tg\alpha} $$

Ho tg α = k₁ tg β = k₂. Следовательно,

$$ tg\phi = \frac{k_2 - k_1}{1 + k_1 k_2} $$

Так, угол между прямыми у = ^x/₂ (k₁ = ¹/₂) и у =3x (k₂= 3) определяется из условия

$$ tg\phi = \frac{3 - \frac{1}{2}}{1+3\cdot\frac{1}{2}} = 1 $$

Поэтому φ = ^π/₄ .

Формулы для котангенса суммы и разности двух углов можно получить аналогично.