Теорема о трех перпендикулярах. Задачи.

Пусть из точки М, не лежащей в плоскости р, проведены прямая MN, перпендикулярная плоскости р, и некоторая прямая MK, пересекающая плоскость р, но не перпендикулярная ей (рис. 146).

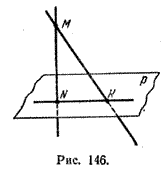
Длина отрезка МN называется длиной перпендикуляра к плоскости р, проходящего через точку М.

Прямая МК называется наклонной к плоскости р, а прямая NK, где N \(\in\) р и К \(\in\) р, называется проекцией этой наклонной на плоскость р.

Длина отрезка МК называется длиной наклонной к плоскости р, а длина отрезка NK - длиной проекции этой наклонной.

Точку пересечения перпендикуляра MN с плоскостью р называют основанием перпендикуляра, а точку пересечения плоскости р и наклонной - основанием наклонной.

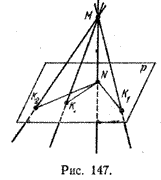
Имеют место следующие свойства:

1) длина перпендикуляра MN (рис. 147) к плоскости р меньше длины любой наклонной МК к плоскости р;

2) длины наклонных МК и МК₁ к плоскости р равны тогда и только тогда, когда равны длины их проекций на эту плоскость;

3) длина наклонной МК меньше длины наклонной МК₂ к плоскости р тогда и только тогда, когда длина проекции наклонной МК на плоскость р меньше длины проекции наклонной МК₂.

Свойство 1) следует из того, что в прямоугольном треугольнике длина гипотенузы больше длины любого катета.

Свойство 2) следует из признаков равенства прямоугольных треугольников. Действительно, если |МК| = |MK₁|, то \(\Delta\)MNK \(\cong\) \(\Delta\)AMNK₁ и поэтому |NK| = |NK₁|. Аналогично, если |NK| = |NK₁|, то \(\Delta\)MNK \(\cong\) \(\Delta\)MNK₁ и |МК| = |MK₁|.

Свойство 3) следует из теоремы Пифагора. Действительно,

|MK|² = |MN|² + |NK|²,

|MK₂|² = |MN|² + | NK₂|²,

и поэтому |МК| < |МК₂| тогда и только тогда, когда |NK| < |NK₂|.

Свойство 1) наклонной и перпендикуляра к плоскости делает естественным следующее определение расстояния от точки до плоскости.

Для любой точки М, не лежащей в плоскости р, длина отрезка MN перпендикуляра к плоскости р, N \(\in\) р, проходящего через точку М, называется расстоянием от точки М до плоскости р. Расстояние от точки М\(\in\) р до плоскости р считается равным нулю.

Задача 1. Катеты прямоугольного треугольника ABC (С =90°) равны 4 см и 3 см. Точка М находится на расстоянии √6 см от плоскости треугольника ABC и на одинаковом расстоянии от всех его вершин. Найти расстояние от точки М до вершин треугольника.

Расстояние от точки М до плоскости треугольника ABC есть длина перпендикуляра, проведенного через точку М к этой плоскости, а расстояния от точки М до вершин - длины соответствующих наклонных (рис. 148).

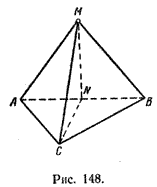
Так как |МА| = |MB| = |МС|, то длины проекций этих наклонных также равны. Поэтому основанием перпендикуляра MN является середина гипотенузы треугольника ABC.

Из \(\Delta\)АВС имеем | АВ| = √16 + 9 = 5 (см). Из \(\Delta\)MNA имеем |МА| = √6,25 + 6 = 3,5 (см).

Теорема. Для того чтобы прямая l \(\subset\) р была перпендикулярна наклонной к плоскости р, необходимо и достаточно, чтобы прямая l была перпендикулярна проекции наклонной (на плоскость р).

Эта теорема называется теоремой о трех перпендикулярах.

Пусть (MN) ⊥ р, (МК) - наклонная, (NК) - проекция наклонной на плоскость р (рис. 149).

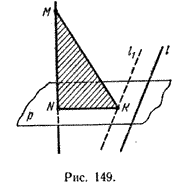
Докажем сначала следующее утверждение (достаточность): если l ⊥ (NK), то l ⊥ (МК).

Так как l ⊥ (MN) и l ⊥ (NK), то, в силу признака перпендикулярности прямой и плоскости, прямая l перпендикулярна плоскости MNK, и поэтому l ⊥ (МК) (на рис. 146 l || l₁).

Докажем теперь обратное утверждение (необходимость): если l ⊥ (МК), то l ⊥ (NK).

Так как l ⊥ (MN) и l ⊥ (МК), то прямая l перпендикулярна плоскости MNK и, следовательно, l ⊥ (NK).

Задача 2. Доказать, что величина угла между наклонной МК к плоскости р и прямой AK, лежащей в плоскости р и проходящей через основание наклонной, будет наименьшей, когда (АК) - проекция наклонной МК на плоскость р.

Пусть N - основание перпендикуляра MN к плоскости р. Из точки N в плоскости р проведем перпендикуляр NB к прямой АК (рис. 150).

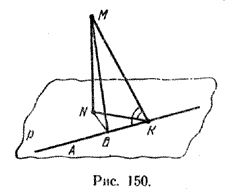
Из теоремы о трех перпендикулярах следует, что (MB) ⊥ (АК). Из прямоугольных треугольников MNK, MNB и МВК получаем

$$ sin\widehat{MKN}=\frac{\left|MN\right|}{\left|MK\right|} < \frac{\left|MB\right|}{\left|MK\right|}=sin\widehat{MKB} $$

и поэтому \(\widehat{MKN} < \widehat{MKB}\), что и требовалось доказать.

Угол между наклонной l к плоскости р и ее проекцией на эту плоскость называется углом между прямой l и плоскостью р и обозначается \(\widehat{(l;p)}\). Если l - наклонная к р, то, согласно определению, 0 < \(\widehat{(l;p)}\) < ^π/₂. Полагают:\(\widehat{(l;p)}\) = 0, если l || р и \(\widehat{(l;p)}\) = ^π/₂, если l ⊥ р.

Таким образом, угол между прямой l и плоскостью р определен во всех случаях. Причем всегда 0 < \(\widehat{(l;p)}\) < ^π/₂ если угол измеряется в радианах, и 0° < \(\widehat{(l;p)}\) < ^π/₂ 90°, если угол измеряется в градусах.

Из рис. 151 видно, что если 1 = (МК) - наклонная к плоскости р, а m = (MN) - перпендикуляр к р, то \(\widehat{(l;p)}\) = ^π/₂ - \(\widehat{(l;m)}\).

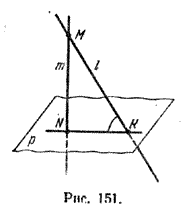
Легко видеть, что эта формула справедлива и в других случаях, т. е. когда l || р или l ⊥ р.

Задача 3. Из вершины А прямоугольного треугольника ABC (С = 90°) проведен перпендикуляр AD к его плоскости. Найти расстояние от точки D до катета ВС, если |ВС| = m, |DB| = n.

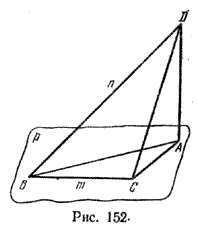
Так как (AD) ⊥ р, то (DC) - наклонная (рис. 152), а (АС) - проекция этой наклонной на плоскость р. По теореме о трех перпендикулярах (DC) ⊥ (ВС), так как (ВС) ⊥ (АС) по условию. Из прямоугольного треугольника BCD находим: |CD| = \(\sqrt{n^2 - m^2}\). Это и есть расстояние от точки D до катета ВС.