Сравнение отрезков. Действия над отрезками.

Равные и неравные отрезки

Отрезки называются равными, если они могут быть наложены один на другой так, что концы их совпадут.

Пусть нам даны два отрезка АВ и СD (рис.). Наложим отрезок АВ на отрезок CD так, чтобы точка А совпала с точкой С, и отрезок АВ направим по отрезку CD. Если точка В совпадаете точкой D, то отрезки АВ и CD равны; АВ = CD.

Сравним два отрезка КО и ЕМ (рис.).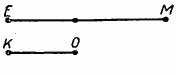

Наложим отрезок КО на отрезок ЕМ так, чтобы точки К и Е совпали. Отрезок КО направим по отрезку ЕМ. Если точка О окажется где-нибудь между точками Е и М, то говорят, что отрезок ЕМ больше отрезка КО; отрезок КО меньше отрезка ЕМ.

Записывается это тaк: ЕМ > КО, КО < ЕМ.

Построение отрезка, равного данному, с помощью циркуля.

Построение отрезка, равного данному отрезку АВ (рис.), выполняется с помощью циркуля таким образом:

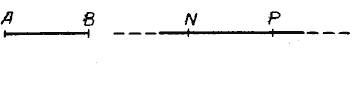
одну ножку циркуля устанавливают на один конец отрезка АВ, а другую — на другой его конец и, не меняя раствора циркуля, переносят его на некоторую прямую так, чтобы конец одной ножки отметил какую-нибудь точку N, тогда конец другой ножки циркуля отметит некоторую точку Р на этой же прямой. Отрезок NP будет равен отрезку АВ.

Сложение и вычитание отрезков.

Чтобы найти сумму двух отрезков, например АВ и СD (рис.), надо взять прямую линию и на ней некоторую точку, например точку N (рис., б), затем с помощью циркуля отложить на этой прямой от точки N сначала отрезок NP, равный отрезку АВ, а потом от его конца в том же направлении отложить отрезок РМ, равный отрезку СD. Отрезок NM будет называться суммой отрезков АВ и СD.

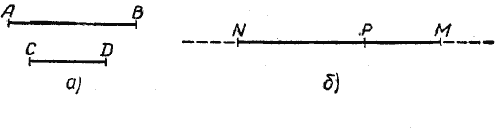
Это записывают так:

NM = АВ + СD.

Таким же образом находится сумма нескольких отрезков (рис.)

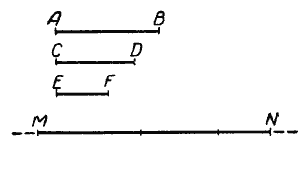
MN = АВ + СD + ЕF.

При сложении отрезков, как и в арифметике при сложении чисел, выполняются законы: переместительный и сочетательный.

АВ + СD = СD + АВ;

(АВ + СD) + ЕF =АВ + (СD + ЕF).

Чтобы найти разность двух отрезков АВ и СD (рис.),

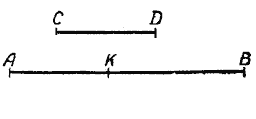
надо на большем отрезке (АВ) от конца его, например точки А, отложить меньший отрезок (СD). Оставшаяся часть (КB) большего отрезка и будет разностью этих отрезков:

АВ — СD = КВ.

Умножение и деление отрезка на целое число.

а) Умножить отрезок AB на целое число, например на 5, это значит, что отрезок АВ надо взять слагаемым 5 раз (рис.):

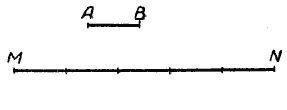
5АВ = МN.

Отрезок МN есть произведение отрезка АВ на число 5.

б) На рисунке отрезок МN составлен из пяти равных отрезков, т. е. отрезок МN разделён на пять равных частей. Каждый из них составляет ¹/₅ часть отрезка МN.

в) Чтобы разделить отрезок на равные части с помощью циркуля, поступают таким образом. Например, если нужно разделить отрезок на две равные части, то циркуль раздвигают на глаз так, чтобы раствор циркуля составлял примерно половину отрезка. Затем на данном отрезке от его конца последовательно один за другим откладывают этим раствором циркуля два отрезка. Если полученная сумма отрезков будет меньше данного отрезка, тo раствор циркуля увеличивают; если сумма окажется больше данного отрезка, то раствор циркуля уменьшают. Так, постепенно исправляя ошибку, можно отыскать довольно точнo половину отрезка (рис.).

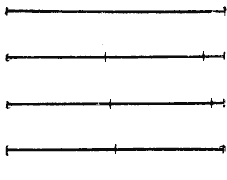
Таким же образом выполняется приближённое деление отрезка на 3, 4, 5 и т. д. равных частей. Только в этом случае надо брать на глаз ¹/₃; ¹/₄; ¹/₅ ... отрезка и откладывать взятый отрезок 3, 4, 5... раз, смотря по тому, на сколько равных частей надо разделить данный отрезок.

Свойство отрезков, отсекаемых параллельными прямыми на сторонах угла

Теорема. Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие другую сторону угла, то и на этой стороне угла отложатся равные между собой отрезки.

Пусть на стороне АВ угла АВN отложены равные отрезки ВМ = МК = КС (рис.) и через точки деления М, К и С проведены параллельные прямые, пересекающие сторону ВN того же угла.

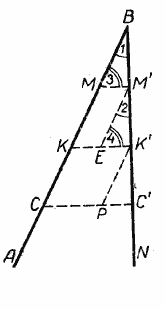
На этой стороне образовались три отрезка: ВМ’, М’К’ и К’С’. Требуется доказать, что ВМ’ = М’К’ = К’С’.

Для доказательства через точки М’ и К’ проведём прямые, параллельные АВ. Мы получим треугольники ВММ’, М’ЕК’ и К’РС’. Сравним эти треугольники.

Сначала сравним треугольники МВМ’ и М’ЕК’. В этих треугольниках имеем:

∠1 = ∠2, как соответственные углы при параллельных ВА и М’Е и секущей ВN;

∠3 = ∠4, как острые углы¹ с соответственно параллельными сторонами (АВ || М’Е и ММ’ || КК’).

ВМ = МК по построению;

МК = М’Е, как противоположные стороны параллелограмма.

Углы 1-й и 4-й могут оказаться оба тупыми, но и в этом случае они останутся равными, а потому доказательство теоремы не изменится.

Следовательно, ВМ = М’Е. Таким образом, ΔВММ’ = ΔМ’ЕК’ (по стороне и двум прилежащим к ней углам). Отсюда следует, что ВМ’ = М’К’.

Так же можно доказать, что ВМ’ = К’С’, т. е. ВМ’ = М’К’ = К’С’. При доказательстве теоремы мы откладывание отрезков начали от вершины угла, но теорема справедлива и для того случая, когда откладывание отрезков будет начато не от вершины угла, а от любой точки его стороны.

В этом случае вершину угла на чертеже можно не отмечать (рис.).

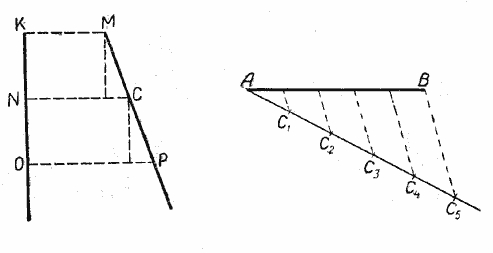
Теорема справедлива и для случая, когда прямые КО и МР параллельны.

Пропорциональные отрезки

Из арифметики известно, что равенство двух отношений называется пропорцией. Например: ¹⁶/₄ = ²⁰/₅; ²/₃ = ⁴/₆ To же самое имеем и в геометрии: если даны две пары отрезков, отношения которых равны, то можно составить пропорцию.

Eсли ^a/_b = ⁴/₃ и ^c/_d = ⁴/₃ (черт. 351), то получим пропорцию ^a/_b = ^c/_d;

отрезки а, b, c, d называются пропорциональными.

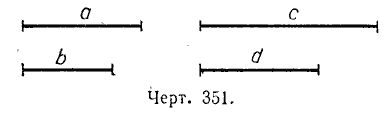
Отношение ^a/_b называется, как и в арифметике, первым отношением, ^c/_d - вторым отношением; а и d называются крайними членами пропорции, b и с — средними членами.

В пропорции можно поменять местами отношения; можно переставить крайние члены, средние члены; можно переставить те и другие одновременно.

Поскольку в пропорции ^a/_b = ^c/_d под буквами подразумевают числа, выражающие длины отрезков, то произведение крайних членов её равно произведению средних членов. Отсюда, зная три члена пропорции, можно найти неизвестный четвёртый её член. Так, в пропорции ^a/_x = ^c/_d x = ^{a • d}/_c

Отметим ещё некоторые свойства пропорций, которыми придётся в дальнейшем пользоваться при доказательстве некоторых теорем и при решении задач.

а) Если три члена одной пропорции соответственно равны трём членам другой пропорции, то равны и четвёртые члены этих пропорций.

Если ^a/_b = ^c/_x и ^a/_b = ^c/_y ,то х = у. В самом деле, x = ^{b • c}/_a , у = ^{b • c}/_a , т. е. и х и у равны одному и тому же числу ^{b • c}/_a .

б) Если в пропорции равны предыдущие члены, то равны и последующие, т. е. если ^a/_x = ^a/_y , то х = у.

Чтобы убедиться в этом, переставим средние члены в этой пропорции.

Получим: ^a/_a = ^x/_y. Но ^a/_a = 1. Следовательно, и ^x/_y = 1.

А это возможно лишь в том случае, когда числитель и знаменатель дроби равны, т. е.

х = у.

в) Если в пропорции равны последующие члены, то равны и предыдущие, т. е. если ^x/_a = ^y/_a , то х = у.

В справедливости этого свойства предлагается вам убедиться самостоятельно. Для этого проведите рассуждение, аналогичное предыдущему.

Построение пропорциональных отрезков

Теорема. Если две прямые пересечь тремя параллельными прямыми, то отношение двух отрезков, получившихся на одной прямой, равно отношению двух соответствующих отрезков другой прямой.

Пусть две прямые ЕF и ОР пересечены тремя параллельными прямыми АВ, СD и МN (рис.).

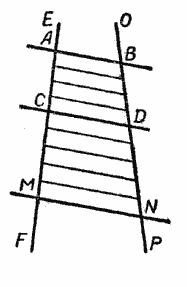
Требуется доказать, что отрезки АС, СМ, ВD и DN, заключённые между параллельными секущими, пропорциональны, т. е.

^AC/_CM = ^BD/_DN

Пусть длина отрезка АС равна р, а длина отрезка СМ равна q.

Например, р = 4 см. и q = 5 см.

Разделим АС и СМ на отрезки, равные 1 см, и из точек деления проведём прямые, параллельные прямым АВ, СD и МN, как это показано на рисунке.

Тогда на прямой ОР отложатся равные между собой отрезки, при этом на отрезке BD их будет 4, а на отрезке DN — 5.

Отношение АС к СМ равно ⁴/₅ , точно так же и отношение ВD к DN равно ⁴/₅.

Отсюда ^AC/_CM = ^BD/_DN.

Значит, отрезки АС, СМ, ВD и DN пропорциональны. Пропорциональны также и отрезки АС, АМ, ВD и ВN (налегающие друг на друга), т. е. ^AC/_AM = ^BD/_BN,

так как ^AC/_AM = ⁴/₉ и ^BD/_BN = ⁴/₉

Теорема будет справедлива и при любых других целых значениях р и q.

Если длины отрезков АС и СМ не выразятся в целых числах при данной единице измерения (например, сантиметре), то надо взять такую более мелкую единицу (например, миллиметр или микрон), при которой длины отрезков АС и СМ практически выразятся в целых числах.

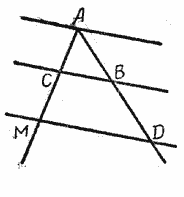
Доказанная теорема справедлива и в том случае, когда одна из параллельных секущих проходит через точку пересечения данных прямых. Она справедлива также и в том случае, когда отрезки откладываются не непосредственно один за другим, а через некоторый промежуток.