Общее уравнение прямой на плоскости

Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

Пусть дана некоторая точка M₀ и вектор n. Проведем через точку M₀ прямую l перпендикулярно вектору n (рис. 82).

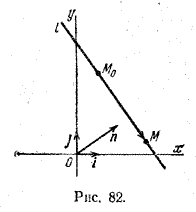
Пусть M - произвольная точка. Точка M лежит на прямой l в том и только в том случае, когда вектор \(\overrightarrow{M_{0}M}\) перпендикулярен вектору n, а для этого необходимо и достаточно, чтобы скалярное произведение векторов n и \(\overrightarrow{M_{0}M}\) равнялось нулю:

n • \(\overrightarrow{M_{0}M}\) = 0. (1)

Чтобы выразить последнее равенство в координатах, введем прямоугольную декартову систему координат. Пусть точки М₀ и М имеют координаты (х₀ ; у₀ ) и (х; у).

Тогда \(\overrightarrow{M_{0}M}\) = (x - x₀; у - у₀). Обозначим координаты нормального вектора n через (А; В). Теперь равенство (1) можно записать так:

А(х - x₀) + В(у - у₀) = 0. (2)

Уравнение (2) есть уравнение прямой l, проходящей через данную точку М₀(х₀; у₀) перпендикулярно данному вектору n = (А; В).

Общее уравнение прямой

Пусть дана произвольная прямая. Выберем на ней некоторую точку М₀(х₀; у₀), и пусть n = (А; В) - произвольный нормальный вектор этой прямой. Тогда (см. § 29) уравнением этой прямой будет уравнение

А(х - х₀) + В(у - у₀) = 0.

Запишем его так:

Ах - Ах₀ + Bу - Bу₀ = 0.

Обозначив число - (Ах₀ + Ву₀) через С, получим

Ах + Bу + С = 0. (1)

Таким образом, всякая прямая плоскости определяется уравнением (1), т. е. линейным уравнением с двумя переменными.

Докажем теперь, что всякое линейное уравнение является уравнением прямой.

В самом деле, в уравнении (1) по крайней мере один из коэффициентов А или В отличен от нуля, иначе это уравнение не будет линейным. Пусть, например, В =/= 0, тогда уравнение (1) можно записать в виде

A(х - 0) + B (y + ^C/_B) = 0. (2)

Согласно уравнению прямой, проходящей через данную точку перпендикулярно данному вектору, уравнение (2), а следовательно, и уравнение (1) определяют прямую, проходящую через точку (0; -^C/_B) и перпендикулярную вектору n = (А; В).

Уравнение Ах + Bу + С = 0 называется общим уравнением прямой.

Отметим, что в уравнении Ах + Bу + С = 0 коэффициент А при переменной х является первой координатой нормального вектора прямой, а коэффициент В при переменной у - второй координатой нормального вектора прямой.