Взаимное расположение прямых в пространстве

В пространстве две различные прямые могут лежать или не лежать в одной плоскости. Рассмотрим соответствующие примеры.

Пусть точки А, В, С не лежат на одной прямой. Проведем через них плоскость р и выберем некоторую точку S, не принадлежащую плоскости р (рис. 130).

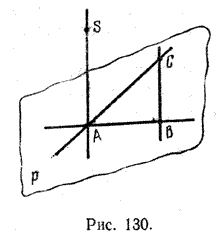
Тогда прямые АВ и ВС лежат в одной плоскости, именно в плоскости р, прямые AS и СВ не лежат в одной плоскости. Действительно, если бы они лежали в одной плоскости, то и точки А, В, С, S лежали бы в этой плоскости, что невозможно, так как S не лежит в плоскости, проходящей через точки А, В, С.

Две различные прямые, лежащие в одной плоскости и не пересекающиеся, называются параллельными. Совпадающие прямые также называются параллельными. Если прямые l₁ и l₂ параллельные, то пишут l₁ || l₂.

Таким образом, l₁ || l₂, если, во-первых, существует плоскость р такая, что

1₁ \( \subset \) р и l₂ \( \subset \) р и, во-вторых, или l₁ \( \cap \) l₂ = \(\varnothing \) или l₁ = l₂.

Две прямые, не лежащие в одной плоскости, называются скрещивающимися. Очевидно, скрещивающиеся прямые не пересекаются и не являются параллельными.

Докажем одно важное свойство параллельных прямых, которое называется транзитивностью параллельности.

Теорема. Если две прямые параллельны третьей, то они параллельны между собой.

Пусть l₁ || l₂ и l₂ || l₃. Нужно доказать, что l₁ || l₃

Если прямые l₁, l₂, l₃ лежат в одной плоскости, то это утверждение доказано в планиметрии. Будем предполагать, что прямые l₁, l₂, l₃ не лежат в одной плоскости.

Через прямые l₁ и l₂ проведем плоскость р₁, а через l₂ и l₃ - плоскость р₂ (рис. 131).

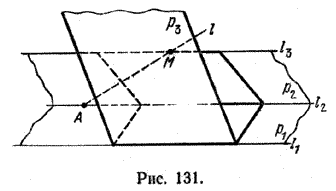
Заметим, что прямая l₃ содержит хотя бы одну точку М, не принадлежащую плоскости р₁.

Через прямую и точку М проведем плоскость р₃, которая пересечется с плоскостью р₂ по некоторой прямой l. Докажем, что l совпадает с l₃. Доказывать будем «методом от противного».

Предположим, что прямая l не совпадает с прямой l₃. Тогда l пересекает прямую l₂ в некоторой точке A. Отсюда следует, что плоскость р₃ проходит через точку А \( \in \) р₁ и прямую l₁ \( \subset \)р₁ и, следовательно, совпадает с плоскостью р₁. Этот вывод противоречит тому, что точка М \( \in \) р₃ не принадлежит плоскости р₁.

Следовательно, наше предположение неверное, и поэтому l = l₃.

Таким образом, доказано, что прямые l₁ и l₃ лежат в одной плоскости р₃.

Докажем, что прямые l₁ и l₃ не пересекаются.

Действительно, если бы l₁ и l₃ пересекались, например, в точке В, то плоскость р₂ проходила бы через прямую l₂ и через точку В \( \in \) l₁ и, следовательно, совпадала бы с р₁, что невозможно.

Задача. Доказать, что углы с сонаправленными сторонами имеют равные величины.

Пусть углы MAN и M₁A₁N₁ имеют сонаправленные стороны: луч AM сонаправлен лучу А₁М₁, а луч AN сонаправлен лучу A₁N₁ (рис. 132).

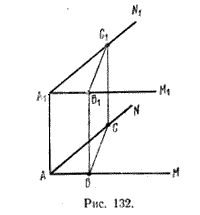
На лучах AM и А₁М₁ отложим равные по длине отрезки АВ и А₁В₁. Тогда

[BB₁] || [AA₁] и |BB₁| = |AA₁|

как противоположные стороны параллелограмма.

Аналогично, на лучах AN и A₁N₁ отложим равные по длине отрезки АС и А₁С₁ . Тогда

[CC₁] || [AA₁] и |CC₁| = |AA₁|

Из транзитивности параллельности следует, что [BB₁] || [CC₁]. А так как |BB₁| = |CC₁| , то BB₁C₁C - параллелограмм, и поэтому |ВС| = |B₁C₁|.

Следовательно, \(\Delta ABC \cong \Delta\)А₁В₁С₁ и \( \widehat{BAC}=\widehat{B_{1}A_{1}C_{1}} \).