Нормированное уравнение прямой
Пусть l - произвольная прямая (рис. 102).
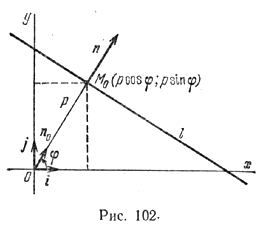
Обозначим через p расстояние от начала координат до прямой l, а через φ - угол между осью Ох и нормальным вектором прямой l. Угол будем отсчитывать от оси Оx в направлении, противоположном движению часовой стрелки. Очевидно, что положение прямой на плоскости полностью определяется заданием величин p и φ. Выразим коэффициенты уравнения прямой l через p и φ.
Пусть M0 - точка пересечения прямой l и перпендикулярной ей прямой, проходящей через начало координат, n0 - единичный нормальный вектор прямой l, т. е. |n0| = 1. Координаты точки M0 и вектора n0 выражаются через заданные величины p и φ следующим образом:
M0(p cos φ; p sinφ), n0 = (cos φ; sinφ).
Известно уравнение прямой, проходящей через точку (х0; у0) с нормальным вектором {А; В):
А(x - x0) + В(у - у0) = 0.
Подставив в это уравнение координаты точки M0 и вектора n0, получим
cos φ {x - p cos φ) + sin φ (у - р sin φ) = 0,
или
х cos φ + у sin φ - р (cos2 φ + sin2 φ) = 0.
В результате приходим к уравнению
х cos φ + у sin φ - р = 0.
Оно называется нормированным уравнением прямой.
В нормированном уравнении все коэффициенты имеют геометрический смысл: коэффициенты при переменных х и у - координаты единичного нормального вектора прямой; свободный член (-р) равен расстоянию от начала координат до прямой, взятому со знаком «минус». Подчеркнем еще раз, что в нормированном уравнении прямой свободный член меньше или равен нулю.
Рассмотрим, например, уравнение х - у + 5√2 = 0. Оно не является нормированным: вектор (1; -1) не единичный, так как | n | =√2 =/=1; свободный член уравнения положителен. Умножим обе части уравнения на (- 1/√2 ). Тогда уравнение прямой примет вид
- x/√2 + y/√2 - 5 = 0
и станет нормированным, так как теперь вектор (- 1/√2 ; 1/√2) очевидно, единичный, а свободный член уравнения отрицателен. Нормальный вектор рассматриваемой прямой образует с осью Оx угол φ такой, что cos φ = - 1/√2 , sin φ = 1/√2 ,
т. е. φ = 135°. Прямая проходит на расстоянии 5 единиц длины от начала координат.
Общее уравнение прямой
Аx + Ву + С = 0
всегда можно привести к нормированному виду (нормировать). Если С < 0, то, умножив обе части уравнения на нормирующий множитель \(\frac{1}{\sqrt{A^2 + B^2}} \), получим уравнение
$$ \frac{A}{\sqrt{A^2 + B^2}}x + \frac{B}{\sqrt{A^2 + B^2}}y + \frac{C}{\sqrt{A^2 + B^2}} = 0 $$которое является нормированным, так как вектор \( (\frac{A}{\sqrt{A^2 + B^2}}; \frac{B}{\sqrt{A^2 + B^2}}) \) как легко проверить - единичный, а свободный член уравнения меньше или равен нулю.
Случай С > 0 сводится к предыдущему умножением обеих частей уравнения на -1. Поэтому, если С > 0, то за нормирующий множитель следует взять число \( -\frac{1}{\sqrt{A^2 + B^2}} \)
Задача. Вычислить расстояние от начала координат до прямой 6x - 8y + 25 = 0.
Тaк как С = 25 > 0, то, умножив обе части уравнения на нормирующий множитель
$$ -\frac{1}{\sqrt{A^2 + B^2}} = -\frac{1}{\sqrt{36 + 64}} = -\frac{1}{10}, $$получим нормированное уравнение данной прямой
- 0,6х + 0,8y - 2,5 = 0.
Учитывая геометрический смысл свободного члена нормированного уравнения прямой, видим, что искомое расстояние равно 2,5.