Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

Пусть дана некоторая точка М₀ и вектор n. Проведем через точку М₀ прямую l перпендикулярно вектору n (рис. 82).

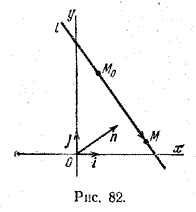
Пусть M - произвольная точка. Точка M лежит на прямой l в том и только в том случае, когда вектор \(\overrightarrow{M_{0}M}\) перпендикулярен вектору n, а для этого необходимо и достаточно, чтобы скалярное произведение векторов n и \(\overrightarrow{M_{0}M}\) равнялось нулю:

n • \(\overrightarrow{M_{0}M}\) = 0. (1)

Чтобы выразить последнее равенство в координатах, введем прямоугольную декартову систему координат. Пусть точки M₀ и M имеют координаты (x₀ ; у₀ ) и (x; у).

Тогда \(\overrightarrow{M_{0}M}\) = (x - x₀; у - у₀). Обозначим координаты нормального вектора n через (А; В). Теперь равенство (1) можно записать так:

А(x - х₀) + В(у - у₀) = 0. (2)

Уравнение (2) есть уравнение прямой l, проходящей через данную точку М₀ (x₀; у₀) перпендикулярно данному вектору n = (А; В).

Задача 1. Составить уравнение прямой, проходящей через точку А (2; -3) перпендикулярно вектору n = (-1;5) (рис.83).

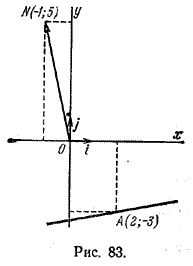
Пользуясь формулой (2), находим уравнение данной прямой:

- 1 • (x-2) + 5 • (у + 3) = 0

или, окончательно, x - 5у - 17 = 0.

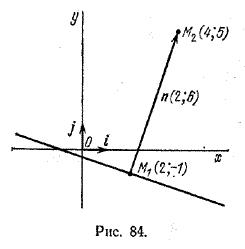
Задача 2. Даны точки M₁(2; -1) и M₂(4; 5). Написать уравнение прямой, проходящей через точку М₁ перпендикулярно вектору \(\overrightarrow{M_{1}M_{2}}\).

Нормальный вектор искомой прямой n = \(\overrightarrow{M_{1}M_{2}}\) имеет координаты (2; 6) (рис. 84).

Следовательно, по формуле (2) получим уравнение

2(x-2) + 6(y+1) = 0

или х + 3y + 1 = 0.

Задача 3. В треугольнике с вершинами в точках M₁(-5; 2), M₂(5; 6) и M₃(1; -2) проведена медиана M₁А₁. Требуется составить уравнение прямой, проходящей через точку А₁ перпендикулярно медиане M₁A₁ (рис. 85).

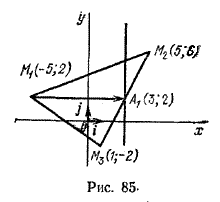
За нормальный вектор искомой прямой можно принять вектор n = \(\overrightarrow{M_{1}A_{1}}\). Определим его координаты. Точка A₁ - середина отрезка M₂M₃, поэтому, если (x₁; y₁) - ее координаты, то \( x_1 = \frac{5+1}{2}=3, \;\;а \;\; y_1=\frac{6-2}{2}=2 \).

Тогда нормальный вектор n = \(\overrightarrow{M_{1}A_{1}}\) имеет координаты (8; 0). Следовательно, искомое уравнение прямой имеет вид

8(x-3) + 0 (y-2) = 0 или x = 3.

Задача 4. Дан треугольник с вершинами в точках А(-3; -1), В(2; 7) и С(5; 4). Требуется составить уравнение прямой, проходящей через вершину С перпендикулярно стороне AB (рис. 86).

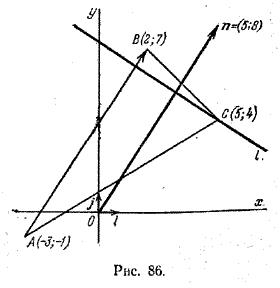
За нормальный вектор искомой прямой можно взять вектор n = \(\overrightarrow{AB}\).

Так как n = (2-(-3); 7 - (-1)) = (5; 8), то, подставляя координаты точки С и координаты вектора n в формулу (2), получим

5(x-5) + 8(y -4) = 0,

или, окончательно, 5х + 8у - 57 = 0.