Уравнение прямой с угловым коэффициентом

Пусть на плоскости, где имеется прямоугольная декартова система координат, прямая l проходит через точку М₀ параллельно направляющему вектору а (рис. 96).

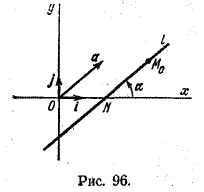
Если прямая l пересекает ось Ох (в точке N), то под углом прямой l с осью Ох будем понимать угол α, на который необходимо повернуть ось Ох вокруг точки N в направлении, обратном вращению часовой стрелки, чтобы ось Ох совпала с прямой l. (Имеется в виду угол, меньший 180°.)

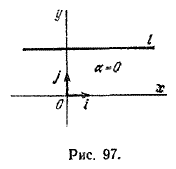
Этот угол называют углом наклона прямой. Если прямая l параллельна оси Ох, то угол наклона принимается равным нулю (рис. 97).

Тангенс угла наклона прямой называется угловым коэффициентом прямой и обычно обозначается буквой k:

tg α = k. (1)

Если α = 0, то и k = 0; это означает, что прямая параллельна оси Ох и ее угловой коэффициент равен нулю.

Если α = 90°, то k = tg α не имеет смысла: это означает, что прямая, перпендикулярная оси Ох (т. е. параллельная оси Оу), не имеет углового коэффициента.

Угловой коэффициент прямой можно вычислить, если известны координаты двух каких-либо точек этой прямой. Пусть даны две точки прямой: M₁(x₁; у₁) и M₂(x₂; у₂) и пусть, например, 0 < α < 90°, а x₂ > x₁, у₂ > у₁ (рис. 98).

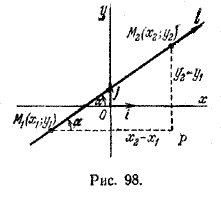
Тогда из прямоугольного треугольника M₁РM₂ находим

$$ k=tga = \frac{|M_2 P|}{|M_1 P|} = \frac{y_2 - y_1}{x_2 - x_1} $$

Итак,

$$ k=\frac{y_2 - y_1}{x_2 - x_1} \;\; (2)$$

Аналогично доказывается, что формула (2) верна и в случае 90° < α < 180°.

Формула (2) теряет смысл, если x₂ - x₁ = 0, т. е. если прямая l параллельна оси Оу. Для таких прямых угловой коэффициент не существует.

***

Задача 1. Определить угловой коэффициент примой, проходящей через точки

M₁(3; -5) и М₂(5; -7).

Подставляя координаты точек M₁ и М₂ в формулу (2), получим

\( k=\frac{-7-(-5)}{5-3} \) или k = -1

Задача 2. Определить угловой коэффициент прямой, проходящей через точки M₁(3; 5) и M₂(3; -2).

Так как x₂ - x₁= 0, то равенство (2) теряет смысл. Для этой прямой угловой коэффициент не существует. Прямая M₁M₂ параллельна оси Оу.

Задача 3. Определить угловой коэффициент прямой, проходящей через начало координат и точку M₁(3; -5)

В этом случае точка M₂ совпадает с началом координат. Применяя формулу (2), получим

$$ k=\frac{y_2 - y_1}{x_2 - x_1}=\frac{0-(-5)}{0-3}= -\frac{5}{3}; \;\; k= -\frac{5}{3} $$

***

Составим уравнение прямой с угловым коэффициентом k, проходящей через точку

M₁(x₁; у₁). По формуле (2) угловой коэффициент прямой находится по координатам двух ее точек. В нашем случае точка M₁ задана, а в качестве второй точки можно взять любую точку М(х; у) искомой прямой.

Если точка М лежит на прямой, которая проходит через точку M₁ и имеет угловой коэффициент k, то в силу формулы (2) имеем

$$ \frac{y-y_1}{x-x_1}=k \;\; (3) $$

Если же точка М не лежит на прямой, то равенство (3) не выполняется. Следовательно, равенствo (3) и есть уравнение прямой, проходящей через точку M₁(x₁; у₁) с угловым коэффициентом k; это уравнение обычно записывают в виде

y - y₁ = k (x - x₁). (4)

Если прямая пересекает ось Оу в некоторой точке (0; b), то уравнение (4) принимает вид

у - b = k (х- 0),

т.е.

y = kx + b. (5)

Это уравнение называется уравнением прямой с угловым коэффициентом k и начальной ординатой b.

Задача 4. Найти угол наклона прямой √3 х + 3у - 7 = 0.

Приведем данное уравнение к виду

$$ y= =\frac{1}{\sqrt3}x + \frac{7}{3} $$

Следовательно, k = tg α = - ¹/_√3 , откуда α = 150°

Задача 5. Составить уравнение прямой, проходящей через точку Р(3; -4), с угловым коэффициентом k = ²/₅

Подставив k = ²/₅ , x₁ = 3, y₁ = - 4 в уравнение (4), получим

у - (- 4) = ²/₅ (х - 3) или 2х - 5у - 26 = 0.

Задача 6. Составить уравнение прямой, проходящей через точку Q (-3; 4) и составляющей с положительным направлением оси Ох угол 30°.

Если α = 30°, то k = tg 30° = ^√3/₃. Подставив в уравнение (4) значения x₁, y₁ и k, получим

у -4 = ^√3/₃ (x + 3) или √3 x -3y + 12 + 3√3 = 0.