Скрещивающиеся прямые

Две прямые могут быть расположены в пространстве так, что через них нельзя провести плоскость.

Возьмём, например (черт. 4), две такие прямые AB и DE, из которых одна пересекает некоторую плоскость H, а другая лежит на ней, но не проходит через точку (С) пересечения первой прямой и плоскости P.

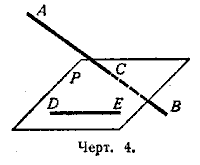
Через такие две прямые нельзя провести плоскость, потому что в противном случае через прямую и точку С проходили бы две различные плоскости: одна P, пересекающая прямую AB, и другая, содержащая её, а это невозможно.

Две прямые, не лежащие в одной плоскости, конечно, не пересекаются, сколько бы их ни продолжали; однако их не называют параллельными, оставляя это название дли таких прямых, которые, находясь в одной плоскости, не пересекаются, сколько бы их ни продолжали.

Две прямые, не лежащие в одной плоскости, называются скрещивающимися.