Угол между прямыми в пространстве

Пусть в пространстве заданы прямые l и m. Через некоторую точку А пространства проведем прямые l₁ || l и m₁ || m (рис. 138).

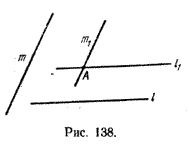
Заметим, что точка А может быть выбрана произвольно, в частности она может лежать на одной из данных прямых. Если прямые l и m пересекаются, то за А можно взять точку пересечения этих прямых (l₁ = l и m₁ = m).

Углом между непараллельными прямыми l и m называется величина наименьшего из смежных углов, образованных пересекающимися прямыми l₁ и m₁ ( l₁ || l , m₁ || m). Угол между параллельными прямыми считается равным нулю.

Угол между прямыми l и m обозначается \( \widehat{(l;m)} \). Из определения следует, что если он измеряется в градусах, то 0°< \( \widehat{(l;m)} \) < 90°, а если в радианах, то 0 < \( \widehat{(l;m)} \) < ^π/₂ .

Задача. Дан куб ABCDA₁B₁C₁D₁ (рис. 139).

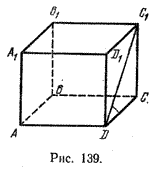
Найти угол между прямыми АВ и DС₁.

Прямые АВ и DС₁ скрещивающиеся. Так как прямая DC параллельна прямой АВ, то угол между прямыми АВ и DС₁, согласно определению, равен \(\widehat{C_{1}DC}\).

Следовательно, \(\widehat{(AB;DC_1)}\) = 45°.

Прямые l и m называются перпендикулярными, если \( \widehat{(l;m)} \) = ^π/₂. Например, в кубе

(см. рис. 139) прямая A₁D₁перпендикулярна прямым DC, DC₁, СС₁ .

Вычисление угла между прямыми.

Задача вычисления угла между двумя прямыми в пространстве решается так же, как и на плоскости. Обозначим через φ величину угла между прямыми l₁ и l₂, а через ψ - величину угла между направляющими векторами а и b этих прямых.

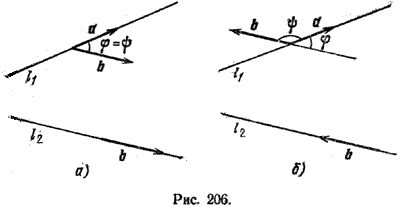
Тогда, если

ψ <90° (рис. 206, а), то φ = ψ; если же ψ > 90° (рис. 206,6), то φ = 180° - ψ. Очевидно, что в обоих случаях верно равенство cos φ = |cos ψ|. По формуле (косинус угла между ненулевыми векторами а и b равен скалярному произведению этих векторов, деленному на произведение их длин) имеем

$$ cos\psi = cos\widehat{(a; b)} = \frac{a\cdot b}{|a|\cdot |b|} $$

следовательно,

$$ cos\phi = \frac{|a\cdot b|}{|a|\cdot |b|} $$

Пусть прямые заданы своими каноническими уравнениями

$$ \frac{x-x_1}{a_1}=\frac{y-y_1}{a_2}=\frac{z-z_1}{a_3} \;\; и \;\; \frac{x-x_2}{b_1}=\frac{y-y_2}{b_2}=\frac{z-z_2}{b_3} $$

Тогда угол φ между прямыми определяется с помощью формулы

$$ cos\phi = \frac{|a_{1}b_1+a_{2}b_2+a_{3}b_3|}{\sqrt{{a_1}^2+{a_2}^2+{a_3}^2}\sqrt{{b_1}^2+{b_2}^2+{b_3}^2}} (1)$$

Если одна из прямых (или обе) задана не каноничecкими уравнениями, то для вычисления угла нужно найти координаты направляющих векторов этих прямых, а затем воспользоваться формулой (1).

Задача 1. Вычислить угол между прямыми

$$ \frac{x+3}{-\sqrt2}=\frac{y}{\sqrt2}=\frac{z-7}{-2} \;\;и\;\; \frac{x}{\sqrt3}=\frac{y+1}{\sqrt3}=\frac{z-1}{\sqrt6} $$

Направляющие векторы прямых имеют координаты:

а = (-√2 ; √2 ; -2), b = (√3; √3; √6).

По формуле (1) находим

$$ cos\phi = \frac{|-\sqrt6+\sqrt6-2\sqrt6|}{\sqrt{2+2+4}\sqrt{3+3+6}}=\frac{2\sqrt6}{2\sqrt2\cdot 2\sqrt3}=\frac{1}{2} $$

Следовательно, угол между данными прямыми равен 60°.

Задача 2. Вычислить угол между прямыми

$$ \begin{cases}3x-12z+7=0\\x+y-3z-1=0\end{cases} и \begin{cases}4x-y+z=0\\y+z+1=0\end{cases} $$

За направляющий вектор а первой прямой возьмем векторное произведение нормальных векторов n₁ = (3; 0; -12) и n₂ = (1; 1; -3) плоскостей, задающих эту прямую. По формуле \( [a; b]=\begin{vmatrix} i & j & k \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix} \) получаем

$$ a=[n_1; n_2]=\begin{vmatrix} i & j & k \\ 3 & 0 & -12 \\ 1 & 1 & -3 \end{vmatrix}=12i-3i+3k $$

Аналогично находим направляющий вектор второй прямой:

$$ b=\begin{vmatrix} i & j & k \\ 4 & -1 & 1 \\ 0 & 1 & 1 \end{vmatrix}=-2i-4i+4k $$

Но формуле (1) вычисляем косинус искомого угла:

$$ cos\phi = \frac{|12\cdot (-2)-3(-4)+3\cdot 4|}{\sqrt{12^2+3^2+3^2}\sqrt{2^2+4^2+4^2}}=0 $$

Следовательно, угол между данными прямыми равен 90°.

Задача 3. В треугольной пирамиде МАВС ребра MA, MB и МС взаимно перпендикулярны, (рис. 207);

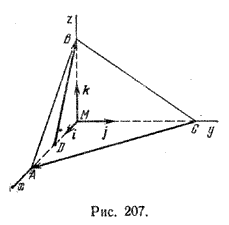
их длины соответственно равны 4, 3, 6. Точка D - середина [МА]. Найти угол φ между прямыми СА и DB.

Пусть СА и DB - направляющие векторы прямых СА и DB.

Примем точку М за начало координат. По условию зядачи имеем А (4; 0; 0), В(0; 0; 3), С(0; 6; 0), D (2; 0; 0). Поэтому \(\overrightarrow{CA}\) = (4; - 6;0), \(\overrightarrow{DB}\)= (-2; 0; 3). Воспользуемся формулой (1):

$$ cos\phi=\frac{|4\cdot (-2)+(-6)\cdot 0+0\cdot 3|}{\sqrt{16+36+0}\sqrt{4+0+9}} $$

По таблице косинусов находим, что угол между прямыми СА и DB равен приблизительно 72°.