Ортогональные проекции прямых и отрезков

Рассмотрим некоторую плоскость р и точку М. Ортогональной проекцией точки М на плоскость р называется основание М₀ перпендикуляра к плоскости р, проведенного через точку М (рис. 157). Плоскость р называют в этом случае плоскостью проекции.

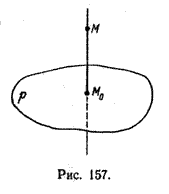
Существует единственный перпендикуляр к плоскости р, проведенный через данную точку. Поэтому для каждой точки пространства существует единственная ортогональная проекция М₀ этой точки на данную плоскость. В частности, если М \(\in\) р, то М₀ = М.

В дальнейшем для краткости, говоря об ортогональных проекциях, мы будем обычно употреблять термин «проекция», опуская слово «ортогональная».

Проекцией прямой l на плоскость р называется множество точек плоскости р, являющихся проекциями точек этой прямой.

Рассмотрим некоторые свойства проекций прямых на плоскость.

1. Если прямая l не перпендикулярна плоскости проекции, то ее проекция на эту плоскость есть прямая.

   Если прямая l лежит в плоскости р, то это утверждение очевидное.

   Пусть прямая l не лежит в плоскости р, и пусть М₀ - проекция точки М, принадлежащей l и не принадлежащей р, на плоскость р (рис. 158).

   

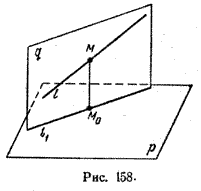
   Через прямые l и М₀М проведем плоскость q. Плоскости р и q перпендикулярны по признаку перпендикулярности плоскостей. Следовательно, прямая l₁ = p \(\cap\) q является проекцией прямой l на плоскость р.

   Отсюда следует, что проекции луча и отрезка (не перпендикулярных плоскости р) представляют собой соответственно луч и отрезок. Если l - перпендикуляр к р, то по определению проекцией l на р будет точка (точка пересечения прямой l и плоскости р).

   Из этого свойства следует, что общее определение проекции прямой на плоскость не противоречит определению проекции наклонной к плоскости.



2. Если прямая l параллельна плоскости проекции, то она параллельна прямой l₁, являющейся ее проекцией.

   

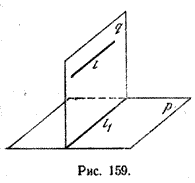
   Действительно, проведя через прямые l и l₁ плоскость q (рис. 159), получим l₁ = p \(\cap\) q Следовательно, l₁ || l.

   Отсюда следует, что проекция отрезка, параллельного плоскости проекции, есть отрезок, конгруэнтный данному.



3. Проекции двух параллельных прямых, не перпендикулярных плоскости проекции, - параллельные прямые.

   

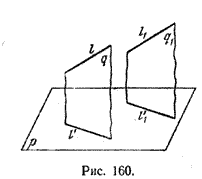
   Пусть плоскость q проходит через прямую l и ее проекцию l’, a q₁ - через прямую l₁ и ее проекцию l’₁ (рис. 160). Плоскости q и q₁ параллельны, так как они перпендикулярны плоскости р и проходят через параллельные прямые l и l₁. Но тогда и l’ || l’₁ как прямые пересечения параллельных плоскостей q , q₁плоскостью р.

   Отсюда следует, что проекции пересекающихся прямых (не лежащих в плоскости, перпендикулярной плоскости р) пересекаются.



4. Отношение длин проекций двух параллельных отрезков, не перпендикулярных плоскости проекции, на данную плоскость равно отношению длин проектируемых отрезков.

Вместо данных отрезков можно рассматривать конгруэнтные им отрезки, лежащие на одной прямой. А так как прямая и ее проекция принадлежат одной плоскости, то доказываемое утверждение следует из теоремы о пропорциональных отрезках на плоскости.

Проекцией фигуры F на плоскость р называется множество точек, являющихся проекциями точек фигуры F на эту плоскость.

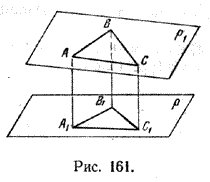
Задача 1. Изобразить проекцию треугольника ABC на данную плоскость р.

Если плоскость \(\Delta\) АВС (p₁) не перпендикулярна плоскости р, то проекцией треугольника ABC на эту плоскость будет некоторый треугольник A₁B₁C₁ (проекция отрезка есть отрезок) (рис. 161).

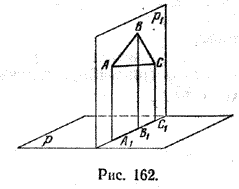
Если p₁ ⊥ p, то проекцией данного треугольника ABC на плоскость р будет отрезок

A₁C₁ (рис. 162).

Если p₁ || p , то проекцией \(\Delta\) АВС на плоскость р будет \(\Delta\) A₁B₁C₁ \(\cong\) \(\Delta\) АВС.

Задача 2. Одна из диагоналей ромба ABCD перпендикулярна данной плоскости р. Какова проекция данного ромба на эту плоскость?

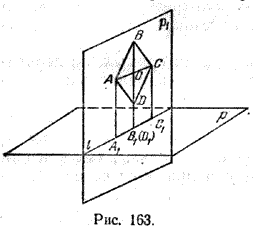
Пусть [BD] ⊥ р (рис. 163).

Тогда плоскость ромба ABCD (p₁) перпендикулярна плоскости р, а проекция [A₁C₁] диагонали АС будет принадлежать l = p₁ \(\cap\) p .

По свойству ромба [AC] ⊥ [BD] , по условию (BD) ⊥ р; по определению прямой, перпендикулярной плоскости, (BD) ⊥ l. Тогда точки В, D и точка О пересечения диагоналей проектируются в точку В₁ (D₁) отрезка A₁C₁. Поэтому проекцией ромба ABCD на плоскость р является отрезок A₁C₁.