Расстояние от точки до прямой

Пусть даны точка M₁(x₁; y₁) и прямая l , заданная своим нормированным уравнением

х cos φ + у sin φ - р = 0.

Найдем расстояние d от точки M₁ до прямой l, т.e. длину отрезка M₁K, где К - проекция точки M₁ на прямую l (рис.).

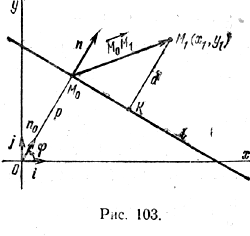
Пусть М₀ (р cos φ; р sin φ) - точка пересечения прямой l с перпендикулярной ей прямой, проходящей через начало координат; n₀ = (cos φ; sin φ) - единичный нормальный вектор прямой l.

Искомое расстояние d равно модулю проекции \(\overrightarrow{M_{0}M_{1}}\) на направление вектора \(\overrightarrow{KM_{1}}\) или, поскольку \(\overrightarrow{KM_{1}}\) и n₀ коллинеарны, на направление вектора n₀ . Итак,

$$ d=|пр_{n_0}\overrightarrow{M_0 M_1}| $$

Выразим проекцию вектора \(\overrightarrow{M_{0}M_{1}}\) на направление вектора n₀ через скалярное произведение этих векторов. Согласно формуле для скалярного произведения 2-х векторов получим

$$ d=|пр_{n_0}\overrightarrow{M_0 M_1}| = |\overrightarrow{M_0 M_1} \cdot n_0| $$

Так как \(\overrightarrow{M_{0}M_{1}}\) = {x₁ - р cos φ; у₁ - р sin φ) и n₀ = (cos φ; sin φ), то

d = | (x₁ - р cos φ)cos φ + (у₁ - р sin φ) sin φ| =

= | x₁ cos φ + у₁ sin φ - p(соs²φ + sin² φ)|

и, окончательно,

d = |x₁ cos φ + у₁ sin φ - p|. (1)

Таким образом, расстояние от точки до прямой равно модулю числа, получающегося, в результате подстановки в левую часть нормированного уравнения прямой координат данной точки.