Свойства касательной

Относительное положение прямой и окружности

Прямая относительно окружности может находиться в следующих трех положениях:

1. Расстояние от центра окружности до прямой больше радиуса. В этом случае все точки прямой лежат вне круга.


2. Расстояние от центра окружности до прямой меньше радиуса. В этом случае прямая имеет точки, лежащие внутри круга и так как прямая бесконечна в обе стороны, то она пересекается сокружностью в 2 точках.


3. Расстояние от центра окружности до прямой равно радиусу. Прямая - касательная.

Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности.

Общая точка называется в этом случае точкой касания.

Возможность существования касательной, и притом проведенной через любую точку окружности, как точку касания, доказывается следующей теоремой.

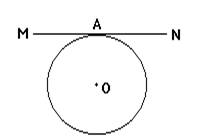
Теорема. Если прямая перпендикулярна к радиусу в его конце, лежащем на окружности, то эта прямая - касательная.

Пусть O (рис) - центр некоторого круга и OA какой-нибудь его радиус. Через его конец A проведем MN ^ OA.

Требуется доказать, что прямая MN - касательная, т.е. что эта прямая имеет с окружностью только одну общую точку A.

Допустим противное: пусть MN имеет с окружностью еще другую общую точку, например B.

Тогда прямая OB была бы радиусом и, следовательно, равнялась бы OA.

Но этого быть не может, так как, если OA -перпендикуляр, то OB должна быть наклонной к MN, а наклонная больше перпендикуляра.

Обратная теорема. Если прямая касательна к окружности, то радиус, проведенный в точку касания, перпендикулярен к ней.

Пусть MN - касательная к окружности, A - точка касания и O - центр этой окружности.

Требуется доказать, что OA^MN.

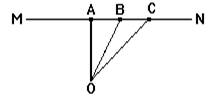
Допустим противное, т.е. предположим, что перпендикуляром, опущенным из O на MN, будет не OA , а какая-нибудь другая прямая, например, OB.

Возьмем BС = AB и проведем OС.

Тогда OA и OС будут наклонные, одинаково удаленные от перпендикуляра OB, и следовательно, OС = OA.

Из этого следует, что окружность, учитывая наше предположение, будет иметь с прямой MN две общие точки: A  и  С , т.е. MN будет не касательная, а секущая, что противоречит условию.

Следствие. Через всякую данную на окружности точку можно провести касательную к этой окружности и притом только одну, так как через эту точку можно провести перпендикуляр, и притом только один, к радиусу, проведенному в нее.

Теорема. Касательная, параллельная хорде, делит в точке касания дугу, стягиваемую хордой, пополам.

Пусть прямая AB (рис.) касается окружности в точке M и параллельна хорде СD.

Требуется доказать, что ÈCM = ÈMD.

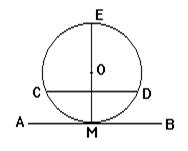
Проведя через точку касания диаметр ME, получаем: EM ^ AB, и следовательно, EM ^ СВ.

Поэтому СM=MD.

Задача. Через данную точку провести касательную к данной окружности.

Если данная точка находится на окружности, то проводят через нее радиус и через конец радиуса перпендикулярную прямую. Эта прямая будет искомой касательной.

Рассмотрим тот случай, когда точка дана вне круга.

Пусть требуется (рис.) провести к окружности с центром O касательную через точку A.

Для этого из точки A, как из центра, описываем дугу радиусом AO, а из точки O, как центра, пересекаем эту дугу в точках B и С раствором циркуля, равным диаметру данного круга.

Проведя затем хорды OB и OС, соединим точку A с точками D и E, в которых эти хорды пересекаются с данной окружностью.

Прямые AD и AE - касательные к окружности O.

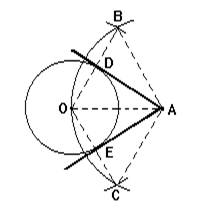
Действительно, из построения видно, что тр-ки AOB и AOС равнобедренные (AO = AB =AС ) с основаниями OB и OС, равными диаметру круга O.

Так как OD и OE - радиусы, то D - середина OB, а E - середина OС, значит AD и AE - медианы, проведенные к основаниям равнобедренных тр-ков, и потому перпендикулярны к этим основаниям. Если же прямые DA и EA перпендикулярны к радиусам OD и OE, то они - касательные.

Следствие. Две касательные, проведенные из одной точки к окружности, равны и образуют равные углы с прямой, соединяющей эту точку с центром.

Так AD=AE и ÐOAD = ÐOAE (рис.), потому что прямоугольные тр-ки AOD и AOE, имеющие общую гипотенузу AO и равные катеты OD и OE (как радиусы), равны.

Заметим, что здесь под словом “касательная” подразумевается собственно “отрезок касательной” от данной точки до точки касания.

Задача. Провести касательную к данной окружности O параллельно данной прямой AB (рис.).

Опускаем на AB из центра O перпендикуляр OС и через точку D, в которой этот перпендикуляр пересекается с окружностью, проводим EF || AB.

Искомая касательная будет EF.

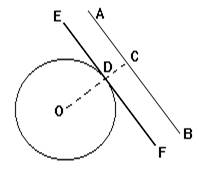
Действительно, так как OС ^ AB и EF || AB, то EF ^ OD, а прямая, перпендикулярная к радиусу в его конце, лежащем на окружности - касательная.

Задача. К двум окружностям O и O₁ провести общую касательную (рис.).

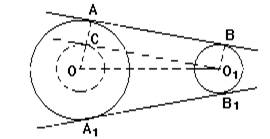
Анализ. Предположим, что задача решена.

Пусть AB будет общая касательная, A и B - точки касания.

Очевидно, что если мы найдем одну из этих точек, например, A, то затем легко найдем и другую.

Проведем радиусы OA и O₁B. Эти радиусы, будучи перпендикулярны к общей касательной, параллельны между собой.

Поэтому, если из O₁ проведем O₁С || BA, то тр-к OСO₁ будет прямоугольный при вершине С.

Вследствие этого, если опишем из O, как центра, радиусом OС окружность, то она будет касаться прямой O₁С в точке С.

Радиус этой вспомогательной окружности известен: он равен OA – СA= OA - O₁B, т.е. он равен разности радиусов данных окружностей.

Построение. Из центра O описываем окружность радиусом, равным разности данных радиусов.

Из O₁ проводим к этой окружности касательную O₁С (способом, указанным в предыдущей задаче).

Через точку касания С проводим радиус OС и продолжаем его до встречи с данной окружностью в точке A. Наконец из A проводим AB параллельно СO_1.

Совершенно таким же способом мы можем построить другую общую касательную A₁B₁ (рис.). Прямые AB и A₁B₁ называют внешними общими касательными.

Можно еще провести две внутренние касательные следующим образом:

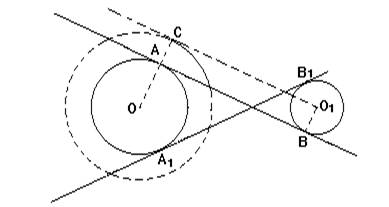
Анализ. Предположим, что задача решена (рис.). Пусть AB - искомая касательная.

Проведем радиусы OA и O₁B в точки касания A и B. Так как эти радиусы оба перпендикулярны к общей касательной, то они параллельны между собой.

Поэтому, если из O₁ проведем O₁С || BA и продолжим OA до точки С, то OС будет перпендикуляр к O₁С.

Вследствие этого окружность, описанная радиусом OС из точки O, как центра, будет касаться прямой O₁С в точке С.

Радиус этой вспомогательной окружности известен: он равен OA+AС = OA+O₁B, т.е. он равен сумме радиусов данных окружностей.

Построение. Из O как центра, описываем окружность радиусом, равным сумме данных радиусов.

Из O₁ проводим к этой окружности касательную O₁С.

Точку касания С соединяем с O.

Наконец через точку A, в которой OС пересекается с данной окружностью, проводим AB = O₁С.

Подобным же способом можем построить другую внутреннюю касательную A₁B₁.

Общее определение касательной

Пусть к окружности с центром (рис.) проведены через точку A касательная AT и какая-нибудь секущая AM.

Станем вращать эту секущую вокруг точки A так, чтобы другая точка пересечения B все ближе и ближе придвигалась к A.

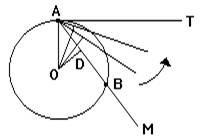
Тогда перпендикуляр OD, опущенный из центра на секущую, будет все больше и больше приближаться к радиусу OA, и угол AOD может стать меньше всякого малого угла.

Угол MAT, образованный секущей и касательной, равен углу AOD (вследствие перпендикулярности их сторон).

Поэтому при неограниченном приближении точки B к A угол MAT также может стать как угодно мал.

Это выражают иными словами так:

касательная есть предельное положение, к которому стремится секущая, проведенная через точку касания, когда вторая точка пересечения неограниченно приближается к точке касания.

Это свойство принимают за определение касательной, когда речь идет о какой угодно кривой.

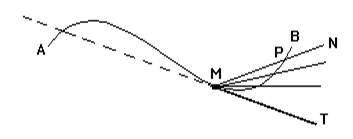
Так, касательной к кривой AB (рис.) называется предельное положение MT, к которому стремится секущая MN, когда точка пересечения P неограниченно приближается к M.

Заметим,что определяемая таким образом касательная может иметь с кривой более одной общей точки (как это видно на рис).