Как найти угол между двумя плоскостями

Рассмотрим две плоскости р₁ и р₂ с нормальными векторами n₁ и n₂. Угол φ между плоскостями р₁ и р₂ выражается через угол ψ = \(\widehat{(n_1; n_2)}\) следующим образом: если ψ < 90°, то φ = ψ (рис. 202, а); если ψ > 90°, то ψ = 180° - ψ (рис. 202,6).

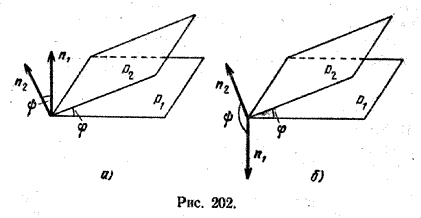
Очевидно, что в любом случае справедливо равенство

cos φ = |cos ψ|

Так как косинус угла между ненулевыми векторами равен скалярному произведению этих векторов, деленному на произведение их длин, имеем

$$ cos\psi=cos\widehat{(n_1; n_2)}=\frac{n_1\cdot n_2}{|n_1|\cdot |n_2|} $$

и, следовательно, косинус угла φ между плоскостями р₁ и р₂ может быть вычислен по формуле

$$ cos\phi=\frac{n_1\cdot n_2}{|n_1|\cdot |n_2|} (1)$$

Если плоскости заданы общими уравнениями

А₁х + B₁y + C₁z + D₁ = 0 и А₂х + B₂y + C₂z + D₂ = 0,

то за их нормальные векторы можно взять векторы n₁ = (A₁; B₁; С₁) и n₂ = (A₂; B₂; С₂).

Записав правую часть формулы (1) через координаты, получим

$$ cos\phi=\frac{|A_1 A_2 + B_1 B-2 + C_1 C_2|}{\sqrt{{A_1}^2+{B_1}^2+{C_1}^2}\sqrt{{A_2}^2+{B_2}^2+{C_2}^2}} $$

Задача 1. Вычислить угол между плоскостями

х - √2 y + z - 2 = 0 и х+ √2 y - z + 13 = 0.

В данном случае A₁.=1, B₁ = - √2 , С₁ = 1, A₂ =1, B₂ = √2, С₂ = - 1.

По формуле (2) получаем

$$ cos\phi=\frac{|1\cdot 1 - \sqrt2 \cdot \sqrt2 - 1 \cdot 1|}{\sqrt{1^2+(-\sqrt2)^2+1^2}\sqrt{1^2+(\sqrt2)^2+(-1)^2}}=\frac{1}{2} $$

Следовательно, угол между данными плоскостями равен 60°.

Плоскости с нормальными векторами n₁ и n₂:

а) параллельны тогда и только тогда, когда векторы n₁ и n₂ коллинеарны;

б) перпендикулярны, тогда и только тогда, когда векторы n₁ и n₂ перпендикулярны, т. е. когда n₁ • n₂ = 0.

Отсюда получаем.необходимые и достаточные условия параллельности и перпендикулярности двух плоскостей, заданных общими уравнениями.

Для того чтобы плоскости

А₁х + B₁y + C₁z + D₁ = 0 и А₂х + B₂y + C₂z + D₂ = 0

были параллельны, необходимо и достаточно, чтобы выполнялись равенства

$$ \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2} \;\; (3)$$

В случае, если какой-либо из коэффициентов A₂, B₂, С₂ равен нулю, подразумевается, что равен нулю и соответствующий коэффициент A₁, B₁, С₁

Невыполнение хотя бы одного из этих двух равенств означает, что плоскости не параллельны, т. е. пересекаются.

Для перпендикулярности плоскостей

А₁х + B₁y + C₁z + D₁ = 0 и А₂х + B₂y + C₂z + D₂ = 0

необходимо и достаточно, чтобы выполнялось равенство

А₁А₂ + B₁B₂ + C₁C₂ = 0. (4)

Задача 2. Среди следующих пар плоскостей:

2х + 5у + 7z - 1 = 0 и 3х - 4у + 2z = 0,

у - 3z + 1 = 0 и 2у - 6z + 5 = 0,

4х + 2у - 4z + 1 = 0 и 2х + у + 2z + 3 = 0

указать параллельные или перпендикулярные. Для первой пары плоскостей

А₁А₂ + B₁B₂ + C₁C₂ = 2 • 3 + 5 • (- 4) + 7•2 = 0,

т. е. выполняется условие перпендикулярности. Плоскости перпендикулярны.

Для второй пары плоскостей

\( \frac{B_1}{B_2}=\frac{C_1}{C_2}\), так как \( \frac{1}{2}=\frac{-3}{-6} \)

а коэффициенты А₁ и А₂ равны нулю. Следовательно, плоскости второй пары параллельны. Для третьей пары

\( \frac{B_1}{B_2}\neq\frac{C_1}{C_2}\), так как \( \frac{2}{1}\neq\frac{-4}{2} \)

и А₁А₂ + B₁B₂ + C₁C₂ = 4•2 + 2•1 - 4•2 =/= 0, т. е. плоскости третьей пары не параллельны и не перпендикулярны.