Условия параллельности и перпендикулярности прямой и плоскости

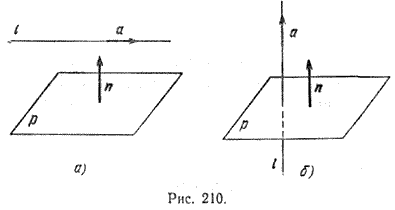
Прямая с направляющим вектором а и плоскость с нормальным вектором n параллельны тогда и только тогда, когда векторы а и n перпендикулярны (рис. 210,а). Для перпендикулярности прямой и плоскости, очевидно, необходимо и достаточно, чтобы векторы а и n были коллинеарны (рис. 210, б).

Если прямая и плоскость заданы уравнениями

$$ \frac{x-x_1}{a_1}=\frac{y-y_1}{a_2}=\frac{z-z_1}{a_3} \;\;и\;\; Ax+By+Cz+D=0 $$

то они:

а) параллельны тогда и только тогда, когда

а₁А + а₂В + а₃С = 0; (2)

б) перпендикулярны тогда и только тогда, когда

\( \frac{a_1}{A}=\frac{a_2}{B}=\frac{a_3}{C} \) (3)

Прямая лежит в плоскости тогда и только тогда, когда она, во-первых, параллельна плоскости и, во-вторых, хотя бы одна ее точка принадлежит плоскости. Поэтому необходимое и достаточное условие принадлежности прямой \(\frac{x-x_1}{a_1}=\frac{y-y_1}{a_2}=\frac{z-z_1}{a_3} \) плоскости Ах +Ву + Сz + D = 0 заключается в выполнении следующих двух равенств:

а₁А + а₂В + а₃С = 0  и  Аx₁ +Ву₁ + Сz₁ + D = 0. (4)