Параллельные плоскости
Определение. Две плоскости называются параллельными, если они не пересекаются, сколько бы их ни продолжали.
Теорема. Если две пересекающиеся прямые (АВ и АС, черт. 8) одной плоскости
(Р) соответственно параллельны двум прямым (А1В1 и А1С1) другой плоскости (Q), то эти плоскости параллельны.
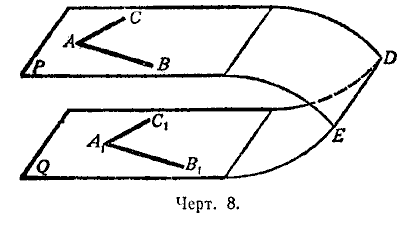
Прямые АВ и АС параллельны плоскости Q.
Допустим, что плоскости Р и Q пересекаются по некоторой прямой DE (черт. 8). В таком случае AB || DE и AC || DE. Таким образом, в плоскости Р через точку А проходят две прямые АВ и АС, параллельные прямой DE, что невозможно. Значит, плоскости Р и Q не пересекаются.
Задача. Построить плоскость, проходящую через заданную точку М параллельно данной плоскости р.
В плоскости р возьмем две пересекающиеся прямые a1 и a2 (рис. 136).
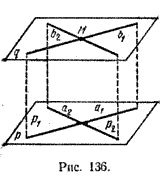
Затем через точку М и прямую a1 проводим плоскость p1 , а через точку М и прямую a2 - плоскость p2.
В плоскости p1 через точку М проведем прямую b1 параллельно прямой a1. Аналогично, в плоскости p2 через М проведем прямую b2 || a2.
Плоскость q, проходящая через пересекающиеся прямые b1 и b2, будет искомой.
Теорема. Если две параллельные плоскости (Р и Q черт. 9) пересекаются третьей плоскостью (R), то линии пересечения (АВ и СD) параллельны.
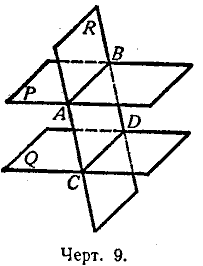
Действительно, во-первых, прямые АВ и СD находятся в одной плоскости (R); во-вторых, они не могут пересечься, так как в противном cлучае пересекались бы плоскости Р и Q, что противоречит условию.
Теорема. Отрезки параллельных прямых (АС и ВD черт. 9), заключённые между параллельными плоскостями (Р и Q), равны.
Через параллельные прямые АС и ВD проведём плоскость R; она пересечёт плоскости Р и Q по параллельным прямым АВ и СD следовательно, фигура АВDС есть параллелограмм, и потому АС || ВD.
Теорема. Два угла (ВАС и В1А1С1, черт. 10) с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях (Р и Q).
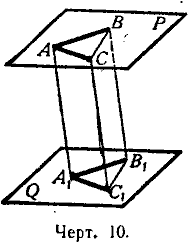
Что плоскости Р и Q параллельны, было доказано выше (§ 15); остаётся доказать, что углы А и А1 равны.
Отложим на сторонах углов произвольные, но равные отрезки АВ = А1В1; АС = А1С1 и проведём прямые АА1, ВВ1, СС1, ВС и В1C1.
Так как отрезки АВ и А1В1 равны и параллельны, то фигура АВВ1А1 есть параллелограмм; поэтому отрезки АА1 и ВВ1 равны и параллельны. По той же причине равны и параллельны отрезки АА1 и СС1, следовательно, ВВ1 || СС1 и ВВ1 = СС1.
Поэтому ВС = В1С1 и \(\Delta\)АВС = \(\Delta\)А1В1С1 (по трём сторонам); значит, ∠А = ∠А1
Теорема. Через точку, не лежащую в данной плоскости, можно провести единственную плоскость, параллельную данной.
Уже доказано, что через точку М, не лежащую в плоскости р, можно провести плоскость q || р.
Докажем методом от противного, что эта плоскость единственная.
Предположим, что через точку М проходят две различные плоскости q и q1 параллельные плоскости р (рис. 137).
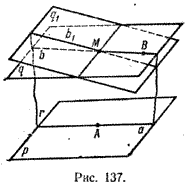
В плоскости q выберем некоторую точку В, не принадлежащую плоскости q1. Через точки М, В и некоторую точку А \(\in\) р проведем плоскость r.
Из первой теоремы следует, что прямая а = р \( \cap \) r параллельна прямой b = q \( \cap \) r и прямой b1 = q1 \( \cap \) r, что невозможно, так как прямые b и b1 пересекаются в точке М.