Прямая, параллельная плоскости

Определение. Плоскость и прямая, не лежащая в этой плоскости, называются параллельными, если они не пересекаются, сколько бы их ни продолжали.

Теорема. Если прямая (АВ, черт. 5) параллельна какой-нибудь прямой (СD), расположенной в плоскости (Р), то она параллельна самой плоскости.

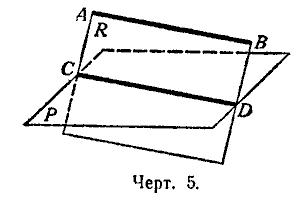
Проведём через АВ и СD плоскость R и предположим, что прямая АВ где-нибудь пересекается с плоскостью Р. Тогда точка пересечения, находясь на прямой АВ, должна принадлежать также и плоскости R, на которой лежит прямая АВ, в то же время точка пересечения, конечно, должна принадлежать и плоскости Р. Значит, точка пересечения, находясь одновременно и на плоскости R и на плоскости Р, должна лежать на прямой СD, по которой пересекаются эти плоскости; следовательно прямая АВ пересекается с прямой СD. Но это невозможно, так как по условию АВ || СD, значит, нельзя допустить, чтобы прямая АВ пересекалась с плоскостью Р, и потому АВ || Р.

Теорема. Если плоскость (R, черт. 5) проходит через прямую (АВ), параллельную другой плоскости (Р), и пересекает эту плоскость, то линия пересечения (СD) параллельна первой прямой (АВ).

Действительно, во-первых, прямая СD лежит в одной плоскости с прямой АВ, во-вторых, эта прямая не может пересечься с прямой АВ, потому что в противном случае прямая АВ пересекалась бы с плоскостью Р, что невозможно.

Следствие 1. Если прямая (АВ, черт. 6) параллельна каждой из двух пересекающихся плоскостей (Р и Q), то она параллельна линии их пересечения (СD).

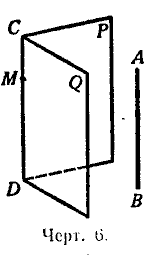
Проведём плоскость через АВ и какую-нибудь точку М прямой СD. Эта плоскость должна пересечься с плоскостями Р и Q по прямым, параллельным АВ и проходящим через точку М. Но через точку М можно провести только одну прямую, параллельную АВ; значит, две линии пересечения проведённой плоскости с плоскостями Р и Q должны слиться в одну прямую. Эта прямая, находясь одновременно на плоскости Р и на плоскости Q, должна совпадать с прямой СD, по которой плоскости Р и Q, пересекаются; значит, СD || AВ.

Следствие 2. Если две прямые (АВ и СD, черт. 7) параллельны третьей прямой

(ЕF), то они параллельны между собой.

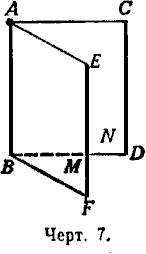
Проведём плоскость М через параллельные прямые АВ и ЕF. Так как СD || EF, то СD || M.

Проведём также плоскость N через СD в некоторую точку А прямой AВ.

Так как EF || СD, то EF || N. Значит, плоскость N должна пересечься с плоскостью M по прямой, параллельной EF и в то же время проходящей через точку А. Но в плоскости М через А проходит единственная прямая, параллельная EF, именно прямая АВ. Следовательно, плоскость N пересекается с М по прямой АВ; значит, СD || AВ.