Перпендикулярные плоскости

Определение. Две плоскости называются взаимно перпендикулярными, если, пересекаясь, они образуют прямые двугранные углы.

Теoрема (выражающая признак перпендикулярности двух плоскостей). Если плоскость (Р, черт. 31) проходит через перпендикуляр (АВ) к другой плоскости (Q), то она перпендикулярна к этой плоскости.

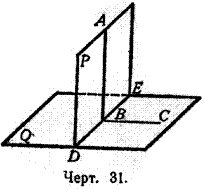
Пусть DE будет линия пересечения плоскостей Р и Q. На плоскости Q проведем

ВС ⊥ DE. Тогда угол ABC будет линейным углом двугранного угла PDEQ.

Так как прямая АВ по условию перпендикулярна к Q, то АВ ⊥ ВС; значит, угол АВС прямой, а потому и двугранный угол прямой, т. е. плоскость Р перпендикулярна к плоскости Q.

Теорема. Если две плоскости (Р и Q, черт. 31) взаимно перпендикулярны и к одной из них (к Q) проведён перпендикуляр (АВ), имеющий общую точку (А) с другой плоскостью (Р), то этот перпендикуляр весь лежит в этой плоскости (Р).

Предположим, что перпендикуляр АВ не лежит в плоскости Р (как изображено на черт. 32).

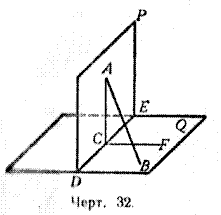
Пусть DE будет линия пересечения плоскостей Р и Q. На плоскости Р проведём прямую AC ⊥ DE, а на плоскости Q проведём прямую CF ⊥ DE. Тогда угол ACF, как линейный угол прямого двугранного угла, будет прямой. Поэтому линия АС, образуя прямые углы с DE и CF, будет перпендикуляром к плоскости Q. Мы будем иметь тогда два перпендикуляра, опущенные из одной и той же точки А на плоскость Q, именно АВ и АС. Так как это невозможно (§ 36), то допущение неверно; значит, перпендикуляр АВ лежит в плоскости Р.

Следствие. Линия пересечения АВ (черт. 33) двух плоскостей (Р и Q), перпендикулярных к третьей плоскости (R), есть перпендикуляр к этой плоскости.

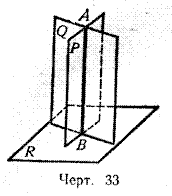
Действительно, если через какую-нибудь точку А линии пересечения плоскостей Р и Q проведём перпендикуляр к плоскости R, то этот перпендикуляр согласно предыдущей теореме должен лежать и в плоскости Q, и в плоскости Р, значит, он сольётся с АВ.