Угол между прямой и плоскостью

Проекция точки и прямой на плоскость.

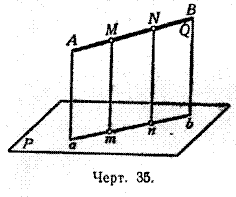
Мы говорили ранее, что когда из одной точки проведены к плоскости перпендикуляр и наклонная, то проекцией этой наклонной на плоскость называется отрезок, соединяющий основание перпендикуляра с основанием наклонной. Дадим теперь более общее определение проекции.

1) Ортогональной (или прямоугольной) проекцией какой-нибудь точки на данную плоскость (например, точки M на плоскость Р, черт. 35) называется основание (m) перпендикуляра, опущенного на эту плоскость из взятой точки.

2) Ортогональной проекцией какой-нибудь линии на плоскость называется геометрическое место проекций всех точек этой линии.

В частности, если проектируемая линия есть прямая (например, АВ, черт. 35), не перпендикулярная к плоскости (Р), то проекция её на эту плоскость есть также прямая. В самом деле, если мы через прямую АВ и перпендикуляр Мт, опущенный на плоскость проекций из какой-нибудь одной точки М этой прямой, проведём плоскость Q, то эта плоскость должна быть перпендикулярна к плоскости Р; поэтому перпендикуляр, опущенный на плоскость P из любой точки прямой АВ (например, из точки М), должен лежать в этой плоскости Q и, следовательно, проекции всех точек прямой АВ должны лежать на прямой аb, по которой пересекаются плоскости Р и Q.

Обратно, всякая точка этой прямой аb есть проекция какой-нибудь точки прямой АВ, так как перпендикуляр, восставленный из любой точки прямой аb, лежит на плоскости следовательно, пересекается с АВ в некоторой точке. Таким образом, прямая аb представляет собой геометрическое место проекций всех точек данной прямой АВ и, следовательно, есть её проекция.

Для краткости речи вместо "ортогональная проекция" мы будем говорить просто "проекция".

Угол прямой с плоскостью

Углом прямой (АВ, черт. 36) с плоскостью (Р) в том случае, когда прямая наклонна к плоскости, называется острый угол (ABC), составленный этой прямой с ee проекцией на плоскость.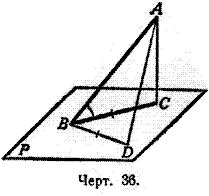

Угол этот обладает тем свойством, что он есть наименьший из всех углов, которые наклонная образует с прямыми, проведёнными на плоскости P через основание наклонной.

Докажем, например, что угол ABC меньше угла ABD.

Для этого отложим отрезок BD = ВС и соединим D с А. У треугольников ABC и ABD две стороны одного равны соответственно двум сторонам другого, но третьи стороны не равны, а именно: AD > АС. Вследствие этого угол ABD больше угла ABC.

Вычисление угла между прямой и плоскостью.
Условия параллельности и перпендикулярности прямой и плоскости

Рассмотрим прямую l с направляющим вектором а и плоскость р с нормальным вектором п. Обозначим через φ угол между прямой l и плоскостью р, а через ψ - угол между векторами а и n. Легко видеть, что φ = 90° - ψ , если ψ < 90° (рис. 209, а) и φ = ψ - 90°, если ψ > 90° (рис. 209,6).

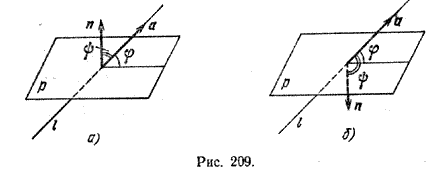
В обоих случаях справедливо равенство sin φ = |cos ψ|.

По формуле (косинус угла между ненулевыми векторами а и b равен скалярному произведению этих векторов, деленному на произведение их длин) находим

$$ cos\psi=cos\widehat{(a; n)}=\frac{a\cdot n}{|a|\cdot |n|} $$

и, следовательно,

$$ sin\phi=\frac{|a\cdot n|}{|a|\cdot |n|} $$

Если известны прямоугольные декартовы координаты направляющего вектора прямой и нормального вектора плоскости a = (a₁; a₂; a₃) и n = (А; В; С), то угол φ может быть вычислен с помощью формулы

$$ sin\phi=\frac{|a_{1}A+a_{2}B+a_{3}C|}{\sqrt{{a_1}^2+{a_2}^2+{a_3}^2}\sqrt{A^2+B^2+C^2}} \;\; (1)$$