Расстояние от точки до плоскости
Найдем расстояние d от произвольной точки М1(х1; у1; z1) до плоскости q, заданной своим нормированным уравнением
х cos α + у cos β + z cos γ - р = 0
Это расстояние равно длине отрезка М1К, где К - проекция точки М1на плоскость q (рис. 205).
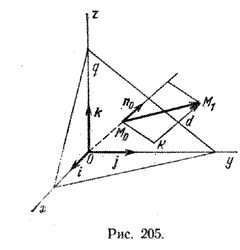
Пусть M0 - точка пересечения плоскости q с перпендикулярной ей прямой, проходящей через начало координат; n0 - единичный нормальный вектор плоскости q. Искомое расстояние d равно модулю проекции вектора \(\overrightarrow{M_{0}M_1}\) на направление вектора \(\overrightarrow{KM_1}\)или, поскольку \(\overrightarrow{KM_1}\) и n0 коллинеарны, на направление вектора n0. Итак,
d = |пpn0 \(\overrightarrow{M_{0}M_1}\)| (1)
Выразим проекцию вектора \(\overrightarrow{M_{0}M_1}\) на направление вектора n0 через скалярное произведение этих векторов.
Согласно формуле (скалярное произведение двух векторов равно произведению длины одного из них и проекции второго вектора на направление первого) получим
d = |пpn0 \(\overrightarrow{M_{0}M_1}\)| = | \(\overrightarrow{M_{0}M_1}\) • n0 |.
Так как \(\overrightarrow{M_{0}M_1}\) = (х1 - р cos α ; y1 - р cos β; z1 - р cos γ) и n0 = (cos α; cos β; cos γ), то
d = | (х1 - р cos α) cos α + (y1 - р cos β) cos β + (z1 - р cos γ) cos γ |
и, следовательно,
d = | х1 cos α +у1 cos β + z1 cos γ - р | (2)
Таким образом, расстояние от точки до плоскости равно модулю числа, получающегося в результате подстановки в левую часть нормированного уравнения плоскости координат данной точки.
Задача 1. Определить расстояние от точки М(0; 1; 1) до плоскости
√23 х - 7у - 3z + 73 = 0.
Нормируем уравнение плоскости. Так как нормирующий множитель равен \( -\frac{1}{\sqrt{23+49+9}}=-\frac{1}{9} \), то получаем
$$ -\frac{\sqrt{23}}{9}x + \frac{7}{9}y + \frac{3}{9}z - \frac{73}{9}=0 $$По формуле (2) находим расстояние
$$ d=\left|-\frac{\sqrt{23}}{9}\cdot 0 + \frac{7}{9}\cdot 1 + \frac{3}{9}\cdot 1 - \frac{73}{9}\right|=\frac{|7+3-73|}{9}=7 $$Задача 2. Найти расстояние между параллельными плоскостями
х - 2y + 2z - 3 = 0 и 2х - 4y + 4z - 30 = 0.
Для определения расстояния между двумя параллельными плоскостями достаточно выбрать на одной из них какую-либо точку и затем найти расстояние от этой гочки до другой плоскости. Точка (15; 0; 0), очевидно, принадлежит второй плоскости. Нормированным уравнением первой плоскости является уравнение
1/3 х - 2/3 y + 2/3 z - 1 = 0
Искомое расстояние d находим по формуле (2);
d = | 1/3 • 15 - 2/3 • 0 + 2/3 • 0 - 1| = 4.