Перпендикуляр к плоскости. Наклонная
Поставим задачу определить, в каком случае прямая может считаться перпендикулярной к плоскости. Докажем предварительно следующее предложение.
Теорема. Если прямая (АА1, черт. 15), пересекающаяся с плоскостью (МN), перпендикулярна к каким-нибудь двум прямым (ОВ и ОС), проведенным на этой плоскости через точку пересечения (O) данной прямой и плоскости, то она перпендикулярна и ко всякой третьей прямой (ОD), проведённой на плоскости через ту же точку пересечения (О).
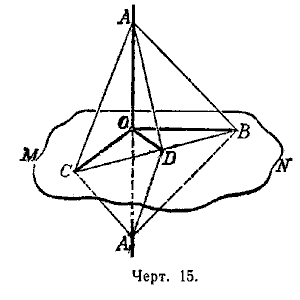
Отложим на прямой АА1 произвольной длины, но равные отрезки ОА и ОА1 и проведём на плоскости какую-нибудь прямую, которая пересекала бы три прямые, исходящие из точки О, в каких-нибудь точках С, D и В. Эти точки соединим с точками А и А1. Мы получим тогда несколько треугольников. Рассмотрим их в такой последовательности.
Сначала возьмём треугольники АСВ и А1СВ; они равны, так как у них СВ—общая сторона, АС=А1С, как наклонные к прямой АА1, одинаково удалённые от основания О перпендикуляра ОС; по той же причине АВ = А1В. Из равенства этих треугольников следует, что ∠ АВС = ∠ А1BС.
После этого перейдём к треугольникам АОВ и А1ОВ; они равны, так как у них ОВ—общая сторона, АВ = А1В и ∠АВD = ∠А1ВD. Из равенства этих треугольников выводим, что АО = А1О.
Теперь возьмём треугольники АОD и А1ОD; они равны, так как имеют соответственно равные стороны. Из их равенства выводим, что ∠АОD и ∠А1ОD , а так как эти углы смежные, то, следовательно, АА1 ⊥ ОD.
Определение. Прямая называется перпендикулярной к плоскости, если она, пересекаясь с этой плоскостью, образует прямой угол с каждой прямой, проведённой на плоскости через точку пересечения. В этом случае говорят также, что плоскость перпендикулярна к прямой.
Из предыдущей теоремы следует, что прямая перпендикулярна к плоскости, если она перпендикулярна к двум прямым, лежащим в данной плоскости и проходящим через точку пересечении данной прямой и плоскости.
Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к этой плоскости. Точка пересечения прямой с плоскостью называется основанием перпендикуляра или наклонной.
Сравнительная длина перпендикуляра и наклонных. Когда из одной точки А (черт. 16) проведены к плоскости перпендикуляр АВ и наклонная АС, условимся называть, проекцией наклонной на плоскость Р отрезок ВС, соединяющий основание перпендикуляра и основание наклонной.
Для краткости термины "перпендикуляр" и "наклонная" употребляются вместо "отрезок перпендикуляра, ограниченный данной точкой и основанием перпендикуляра", и "отрезок наклонной, ограниченный данной точкой и основанием наклонной.
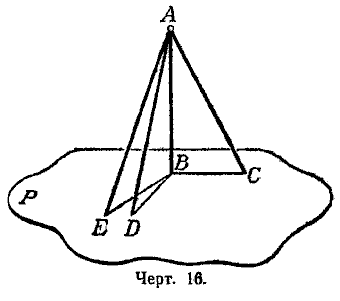
Таким образом, отрезок ВС есть проекция наклонной АС, отрезок ВD есть проекция наклонной АD и т. д.
Теорема. Если из одной и той же точки (А, черт. 16), взятой вне плоскости (Р), проведены и этой плоскости перпендикуляр (AB) и какие-нибудь наклонные (АС, АD, АЕ, ...), то:
1) две наклонные, имеющие равные проекции, равны;
2) из двух наклонных та больше, проекция которой больше,
Вращая прямоугольные треугольники ABC и ABD вокруг катета AB, мы можем совместить их плоскости с плоскостью \(\Delta\)ABE. Тогда все наклонные будут лежать в одной плоскости с перпендикуляром, а все проекции расположатся на одной прямой. Таким образом, доказываемые теоремы приводятся к аналогичным теоремам планиметрии.
Замечание. Так как АВ есть катет прямоугольного треугольника, а каждая из наклонных АС, АD, АЕ, ... есть гипотенуза, то перпендикуляр АВ меньше всякой наклонной; значит, перпендикуляр, опущенный из точки на плоскость, есть наименьший из всех отрезков, соединяющих данную точку с любой точкой плоскости, и потому он принимается за меру расстояния точки А от плоскости Р.
Обратные теоремы. Если из одной и той же точки, взятой вне плоскости, проведены перпендикуляр и какие-нибудь наклонные, то:
1) равные наклонные имеют равные проекции;
2) из двух проекций та больше, которая соответствует большей наклонной.
Доказательство - от противного.
Приведём ещё следующую теорему о перпендикулярах, которая понадобится нам впоследствии.
Теорема. Прямая (DЕ, черт. 17), проведённая на плоскости (Р) через основание наклонной (АС) перпендикулярно к её проекции (ВС), перпендикулярна и к самой наклонной.
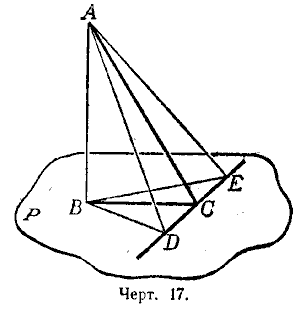
Отложим произвольные, но равные отрезки СD и СЕ и соединим прямолинейными отрезками точки А и В с точками D и E. Тогда будем иметь:
ВD = ВЕ, как наклонные к прямой DЕ, одинаково удалённые от основания С перпендикуляра ВС;
АD = АЕ, как наклонные к плоскости Р, имеющие равные проекции ВD и ВЕ.
Вследствие этого \(\Delta\)АDЕ равнобедренный, и потому его медиана АС перпендикулярна к основанию DЕ.
Эта теорема носит название теоремы о трёх перпендикулярах. Действительно, в ней говорится о связи, соединяющей следующие три перпендикуляра:
1) АВ к плоскости Р,
2) ВС к прямой DE и
3) АС к той же прямой DE.
Обратная теорема. Прямая (ОЕ, черт. 17), проведённая на плоскости (Р) через основание наклонной (АС) перпендикулярно к этой наклонной, перпендикулярна и к её проекции.
Сделаем те же построения, что и при доказательстве прямой теоремы. Отложим произвольные, но равные отрезки СD и СЕ и соединим прямолинейными отрезками точки А и В с точками D и Е, тогда будем иметь:
АD = АЕ, как наклонные к прямой DЕ, одинаково удалённые от основания С перпендикуляра АС;
ВD = ВЕ, как проекции равных наклонных АD и АЕ.
Вследствие этого \(\Delta\)ВDЕ равнобедренный, и потому его медиана ВС перпендикулярна к основанию DЕ.