Признак параллельности прямой и плоскости

Если прямая принадлежит плоскости или не имеет с ней ни одной общей точки, то прямая и плоскость называются параллельными. Если прямая l и плоскость р параллельны, то будем писать l || р. Таким образом, l || р, если l \( \subset \) р или l \( \cap \) p = \(\varnothing \)

Прежде всего докажем одну несложную, но важную теорему.

Теорема 1. Если плоскости р и q пересекаются и прямая 1 \( \subset \) q параллельна плоскости р, то 1 параллельна прямой, являющейся пересечением плоскостей р и q.

Случай, когда l лежит в плоскости l, очевиден, так как тогда l = p \( \cap \) q.

Пусть l не имеет общих точек с р. Тогда, если бы прямые l и l₁ = p \( \cap \) q пересекались, то прямая l пересекалась бы с плоскостью р, что противоречит условию. Следовательно, прямые l и l₁ параллельны.

Докажем теперь следующий признак параллельности прямой и плоскости.

Теорема 2. Для того чтобы прямая l была параллельна плоскости р, необходимо и достаточно, чтобы прямая l была параллельна некоторой прямой, лежащей в плоскости р.

Заметим, что случай, когда l лежит в плоскости p, является очевидным. Поэтому будем рассматривать лишь случай, когда l не лежит в р.

Пусть прямая l и плоскость р параллельны (рис. 133).

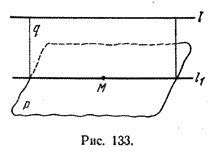
Докажем, что тогда в плоскости р имеется прямая, которая параллельна прямой l . Через прямую l и некоторую точку М \(\in\) р проведем плоскость q. Тогда прямая l параллельна прямой l₁, являющейся пересечением плоскостей р и q.

Докажем теперь обратное утверждение: если в плоскости р есть прямая, параллельная l , то l параллельна р.

Пусть l параллельна прямой l₁ \( \subset \) р. Предположим, что l и р имеют общую точку М₀. Тогда М₀ принадлежит плоскости р и плоскости q, в которой лежат прямые l и l₁ и поэтому М₀ принадлежит прямой l₁ = p \( \cap \) q, что противоречит условию. Следовательно, прямая l и плоскость p не имеют общих точек.