Уравнение плоскости, проходящей через точку перпендикулярно вектору

Пусть дана некоторая точка M₀ и ненулевой вектор n. Через точку M₀ можно провести только одну плоскость р перпендикулярную вектору n (рис. 201).

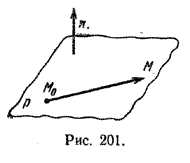
Выведем уравнение плоскости р. Пусть М - произвольная точка пространства. Очевидно, что точка М принадлежит плоскости р тогда и только тогда, когда вектор \(\overrightarrow{M_{0}M}\) перпендикулярен вектору n. Как известно, необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения. Поэтому уравнение плоскости, проходящей через точку M₀ перпендикулярно вектору n, может быть записано в виде

\(\overrightarrow{M_{0}M}\) • n = 0. (1)

Вектор n в уравнении (1) называется нормальным вектором плоскости. В качестве нормального вектора можно взять любой вектор, перпендикулярный плоскости.

Пусть точка M₀ и вектор n заданы своими координатами в некоторой прямоугольной системе координат:

M₀(х₀; у₀; z₀), n = (А; В; С).

Обозначим координаты произвольной точки М плоскости р через х, у и z. Тогда вектор \(\overrightarrow{M_{0}M}\) имеет координаты х - х₀, у - у₀ и z - z₀, а уравнение (1) в координатах записывается следующим образом:

А(х - х₀) + В (у - у₀) + С (z - z₀) = 0. (2)

Это уравнение называется уравнением плоскости, проходящей через точку (х₀; у₀; z₀) перпендикулярно вектору (А; В; С).

Задача 1. Найти уравнение плоскости, проходящей через точку М₀(-3; 4; 7) перпендикулярно вектору n = (1; -2; 6).

В данном случае х₀ = -3, у₀ = 4, z₀ = 7; А = 1, В = -2, С = 6. Подставив эти значения в уравнение (2), получим искомое уравнение

l(x + 3) - 2( y - 4) + 6(z - 7) = 0,

или

х - 2у + 6z - 31 = 0.

3адачa 2. Даны точки M₁ (2; -1; 3) и M₂(4; 5; 0). Написать уравнение плоскости, проходящей через точку М₂ перпендикулярно вектору \(\overrightarrow{M_{1}M_2}\).

За нормальный вектор плоскости можно взять вектор n = \(\overrightarrow{M_{1}M_2}\) = (2; 6; -3). После подстановки координат нормального вектора и координат точки М₀ = М₂(4; 5; 0) в уравнение (2) получим

2 (х - 4) + 6 (y - 5) - 3z = 0

или

2х + 6у - 3z - 38 = 0.

Задача 3. В треугольнике с вершинами в точках А₁{-5; 2; 7), А₂(5; 0; 6), А₃(0; -1; 2) проведена медиана А₁М₀. Найти уравнение плоскости, проходящей через точку М₀ перпендикулярно медиане А₁М₀.

За нормальный вектор плоскости можно принять вектор n = \(\overrightarrow{A_{1}M_0}\). Определим его координаты. Точка М₀ - середина отрезка А₂А₃, поэтому, если (х₀; у₀; z₀) - ее координаты, то

$$ x_0=\frac{5+0}{2}=\frac{5}{2}, \;\; y_0=\frac{0-1}{2}=-\frac{1}{2}, \;\; z_0=\frac{6+2}{2}=4 $$

Координаты нормального вектора n = (А; В; С), следовательно, равны

A = ⁵/₂ + 5 = ¹⁵/₂, В = - ¹/₂ - 2 = - ⁵/₂, С = 4 - 7 = - 3.

Уравнение (2) имеет в данном случае вид

¹⁵/₂ (х - ⁵/₂) - ⁵/₂( y + ¹/₂) - 3 (z - 4) = 0

или

15х -5y - 6z - 16 = 0.