Уравнение плоскости, проходящей через три точки

Плоскость проходит через три данные точки, не лежащие на одной прямой

Пусть точки M₁, M₂, M₃ не лежат на одной прямой. Как известно, три такие точки однозначно определяют некоторую плоскость р (рис. 199).

Выведем уравнение плоскости р. Пусть М - произвольная точка пространства. Очевидно, что точка М принадлежит плоскости р тогда и только тогда, когда векторы

\(\overrightarrow{M_{1}M}\), \(\overrightarrow{M_{1}M_2}\), \(\overrightarrow{M_{1}M_3}\) компланарны. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения (§ 23*, теорема 2). Поэтому уравнение плоскости, проходящей через три точки, не лежащие на одной прямой, может быть записано следующим образом:

(\(\overrightarrow{M_{1}M}\), \(\overrightarrow{M_{1}M_2}\), \(\overrightarrow{M_{1}M_3}\)) = 0. (1)

Если точки M₁, M₂ и M₃ заданы координатами в некоторой прямоугольной декартовой системе координат, то уравнение (1) можно записать в координатах.

Пусть M₁(x₁; y₁; z₁), M₂(х₂; у₂; z₂), M₃(х₃; у₃; z₃) - данные точки. Обозначим координаты произвольной точки М плоскости р через х, у и z. Найдем координаты векторов, входящих в уравнение (1):

\(\overrightarrow{M_{1}M}\) = (х - х₁; у - у₁; z - z₁),

\(\overrightarrow{M_{1}M_2}\) = (x₂ - x₁ ; y₂ - y₁; z₂ - z₁),

\(\overrightarrow{M_{1}M_3}\) = (x₃ - x₁; у₃ - y₁; z₃ - z₁).

Смешанное произведение трех векторов равно определителю третьего порядка, в строках которого стоят координаты векторов. Следовательно, уравнение (1) в координатах имеет вид

$$ \begin{vmatrix} x-x_1 & y-y_1 & z-z_1 \\ x_2-x_1 & y_2-y_1 & z_2-z_1 \\ x_3-x_1 & y_3-y_1 & z_3-z_1 \end{vmatrix}=0 \;\; (2)$$

Найдем уравнение плоскости, проходящей через три точки А (а; 0; 0), В(0; b; 0), С(0; 0;с), у которых а =/= 0, b =/= 0, c =/= 0. Эти точки лежат на осях координат (рис. 200).

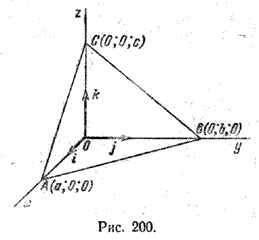
Полагая в уравнении (2) x₁= а, у₁= 0, z₁= 0, x₂= 0, у₂= b, z₂= 0, x₃ = 0, у₃ = 0, z₃ = с, получим

$$ \begin{vmatrix} x-a & y & z \\ -a & b & 0 \\ -a & 0 & c \end{vmatrix}=0 $$

Разложив определитель по элементам первой строки, получим уравнение

bc (х - a) + acy + abz = 0

или

bcx + асу + abz = abc,

^x/_a + ^y/_b + ^z/_c = 1. (3)

Уравнение (3) называется уравнением плоскости в отрезках, так как числа a, b и с указывают, какие отрезки отсекает плоскость на осях координат.

Задача. Написать уравнение плоскости, проходящей через точки M₁(-1; 4; -1), M₂(-13; 2; -10), M₃(6; 0; 12). Упростить полученное уравнение. Получить уравнение данной плоскости в отрезках.

Уравнение (2) в данном случае записывается следующим образом:

$$ \begin{vmatrix} x+1 & y-4 & z+1 \\ -12 & -2 & -9 \\ 7 & -4 & 13 \end{vmatrix}=0 $$

Это и есть уравнение данной плоскости. Разложив определитель по первой строке, получим

- 62(х + 1) +93(y -4)+ 62 (z + 1) = 0,

откуда

- 2x + 3y + 2z - 12 = 0.

Разделив почленно на 12 и перенеся свободный член уравнения в правую часть, получим уравнение данной плоскости в отрезках

$$ \frac{x}{-6}+\frac{y}{4}+\frac{z}{6}=1 $$

Из уравнения видно, что данная плоскость отсекает на осях координат отрезки, длины которых равны соответственно 6, 4 и 6. Ось Ох пересекается плоскостью в точке с отрицательной абсциссой, ось Оу - в точке с положительной ординатой, ось Оz - в точке с положительной апликатой.