В основании призмы ABCA1B1C1 лежит равнобедренный треугольник ABC (AB = AC и / BAC = 2α). Вершина А1 верхнего основания проектируется в центр окружности радиуса R, описанной около нижнего основания. Баковое ребро AA1образует со стороной основания АВ угол, равный 2α. Определить объем и боковую поверхность призмы.
Как в предыдущей задаче, докажем, что ребро АА1⊥ВС (рис.), а следовательно, и ВВ1⊥ВС и грань BB1C1C - прямоугольник.
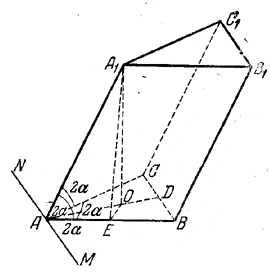
∠ А1АС = ∠ А1АВ = 2α . (доказательство см. в задаче 477) и, следовательно, грань AA1C1C=AA1B1B. Точка Е- середина стороны АВ и EO⊥AB (точка О - центр окружности, описанной около \(\Delta\)АВС); тогда A1E⊥AB (по теореме о трех перпендикулярах). По теореме синусов имеем
AB = 2R sin (90°- α) =2R cos α;
тогда
Socн. = 1/2 АВ2 • sin 2α = 2R2 cos2 α sin 2α.
Из треугольника AA1E имеем
![]()
Из \(\Delta\)AA1O найдем
![]()
(Подкоренное выражение преобразуем, как указано в задаче 464)
Сторона BC = 2BD = 2 • АВ • sin α. Следовательно,
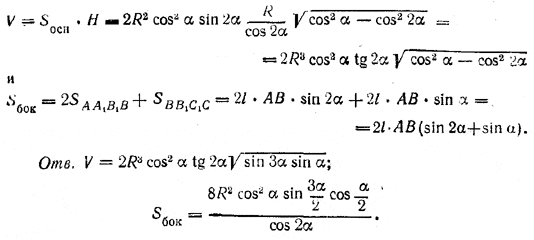
Похожие примеры: