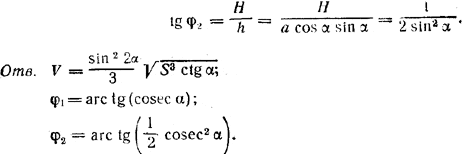В основании пирамиды лежит трапеция, у которой диагональ перпендикулярна к боковой стороне и образует с основанием угол α. Все боковые ребра равны между собой. Боковая грань, проходящая через большее основание трапеции, имеет угол при вершине пирамиды φ= 2α и площадь, равную S. Определить объем пирамиды и углы, под которыми наклонены боковые грани к плоскости основания.
Высота ЕО проходит через центр О окружности, описанной около трапеции ABCD (рис.).
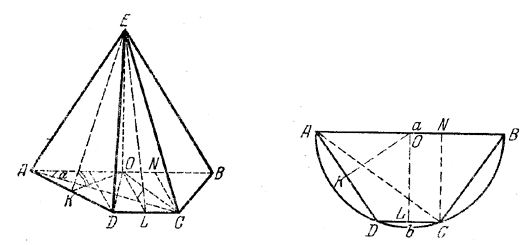
Угол АСВ = 90°, кзк вписанный в эту окружность, должен опираться на диаметр. Иначе говоря, центр О лежит на стороне АВ. Трапеция ABCD, как вписанная в окружность,-равнобочная, так что ∠ DAB = ∠ СВА.
Введем обозначения АВ = а; DC = b, ∠ AEB = φ = 2α. По условию 1/2 аH = S, a из равнобедренного треугольника AЕВ имеем а = 2H tg φ/2 =2H tg α.
Из этих двух уравнений находим
Н =√S ctg α и а = 2 √S tg α.
Сторону b = DC найдем из треугольника ADC, вписанного в окружность с диаметром а. В этом треугольнике
∠ DAC = ∠ DAB - ∠ СAВ = ∠ CBA - ∠ СAВ
Но так как треугольник АСВ - прямоугольный, то ∠ CBA = 90° - ∠ CAB. Следовательно,
∠ DAC = 90° - 2 ∠ CAB = 90° -2α,
и мы имеем
b = a sin (90°- 2α) = a cos2α.
Наконец, находим
CN = h = AC sin α = a cos α sin α.
Теперь получаем
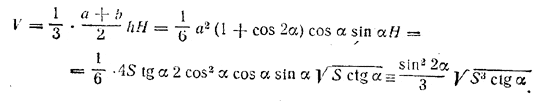
Грань АВE образует с плоскостью ABCD прямой угол. Для определения угла φ1 образуемого гранью ADE с плоскостью ABCD, опустим перпендикуляр из О на AD (он изображается прямой ОК., параллельной диагонали BD, так как последняя перпендикулярна к AD; диагональ BD на чертеже не изображена; ∠ EKO = φ1),
В треугольнике АОК угол OAK равен ∠ AВС = 90° - ∠ CAB = 90° - α. Поэтому
ОК = АО • sin (90° - α) = a/2 cos α
и
![]()
Для определения угла φ2, образуемого гранью DCE с плоскостью ABCD, проводим OL⊥ DC; ∠ ELO = φ2 Так как OL = NC= h, то