В основании пирамиды лежит равнобедренный треугольник с углом αпри основании. Все боковые ребра наклонены к плоскости основания под равными углами φ= 90°— α. Площадь сечения, проведенного через высоту пирамиды и через вершину равнобедренного треугольника, лежащего в основании, равна Q. Определить объем пирамиды.
Точка О есть центр окружности, описанной около основания ABC (рис.)
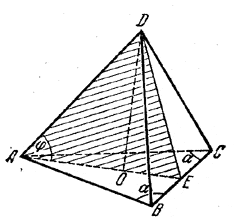
OA = R есть радиус этой окружности. Объем пирамиды
![]()
(так как АE• DO/2 = Q). Сторону ВС находим по теореме синусов:
BC=2R sin(180°-2α) =2R sin 2α.
\(\Delta\)ADO ~ \(\Delta\)ABE (так как ∠ ADO = ∠ ABE = α ); имеем пропорцию:
АO/AE = OD/ВE , откуда АО•ВЕ=АЕ•ОD.
рис. (где АО < АЕ) явно не соответствует этому соотношению. Но чертеж, точнее изображающий условие задачи φ = 90°- α, был бы очень не нагляден.
Подставив сюда
АО = R, BE = BC/2 , АЕ•ОD = Q,
получим
R• ВC/2 = 2Q
Исключив R из найденных формул, получим
ВС = √8Q sin 2α
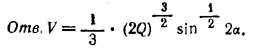
Похожие примеры: